Index A |B |C |D |E |F |G |H |I |K |L |M |N |O |P |Q |R |S |T |U |V |W |Z

A

absolute value

3.3 | 6.1

absolute value (derivative of)

11.1

acceleration

15.2

acceleration due to gravity

15.2

addition law

9.1 | 9.1

addition of points

4.1

addition rule for area

5.2

addition theorem for area

B.

additivity of area

5.1

almost disjoint sets

5.2

Analyst

10.1

and (logical) operator

3.1

antiderivative

12.4 | 17.1

antiderivative theorem

12.4

antidifferentiation, Maple commands

17.1

Apollonius (c 260-170 B.C.)

10.1

approachable point

10.2

approximation

6.2

approximation (strong approximation theorem)

6.2

approximation to 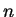$n$ decimals

6.2

arc length

9.1

arccos

14.6

arccot

14.6

Archimedes(287-212 B.C.)

0.1 | 2.2 | 2.3 | 2.4 | 9.1 | 9.2 | 9.2

Archimedes and $\pi$

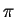
0.3

Archimedes and $\int\sin$

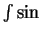
9.3

Archimedes and $\pi$

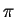
0.3

Archimedes and area of parabolic segment

2.3

arcsin

14.6

arctan

14.6

area = integral

8.6

area as a number

1.

area (assumptions about)

5.1

area between graphs

8.6

area function

5.1 | 5.2

area of box

1.

area of circle

8.5

area of circular sector

17.5

area of ellipse

8.5

area of parabola

2.1 | 2.3

area of parabolic segment

2.3

area of snowflake

2.6

area of triangle

5.3

area under power function

7.2

area, basic assumptions

5.1

Aristotle(384-322 B.C.)

1. | 10.1 | 10.3

Aryabhata (circa 510)

9.1

associative law for points

4.1

assumptions about area

5.1

assumptions: additivity of area

5.1

assumptions: symmetry invariance of area

5.1

assumptions: normalization of area

5.1

assumptions: translation invariance of area

5.1

average velocity

10.3

B

Babylonians

2.2 | 2.2 | 2.4 | 4.3

Babylonians $\pi$

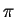
0.3

Banach, Stefan(1892-1945)

5.1

Berkeley, George (1685-1753)

10.1

Bernoulli, Jacob (1654-1705)

2.2 | 6.3 | 6.7

Bernoulli, Daniel(1700-1782)

14.6

between, 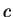$c$ is between 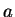$a$ and $b$.

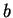14.1

bijective

14.3

Bolzano, Bernard (1781-1848)

10.3 | 14.1

bound for a function

5.1

bounded function

5.1

bounded set

5.1

box

1.

box (circumscribed)

2.1

Brouncker, William(1620-1684)

5.5

C

Cantor, Georg (1845-1918)

1.

Cartesian product.

3.2

Cauchy, Augustin (1789-1857)

3.4 | 10.3

Cavalieri, Bonaventura (1598-1647)

2.5

chain rule

11.3

change of scale for integrals

8.5

chord of an arc

9.1

circle (area of)

8.5

circle (definition of)

4.3

circle (unit)

4.3

circular sector (area of)

17.5

circumscribed box

2.1

circumscribed hexagon for snowflake

2.6

clockwise

9.1

closed interval

1.

codomain

3.3

commutative law for points

4.1

composition of continuous functions

12.1

composition of functions

11.3

composition problem

11.3

compound interest

6.7

computer calculation of area

5.6

congruence problem

5.1

conic section

10.1

conservation of energy

15.2

constant sequence

6.4

constructivists

3.1

continuity defined

12.1

continuity on a set

12.1

contrapositive

3.1

convergent sequence

6.3 | 6.3

convex downward (spills water)

15.3

convex upward (holds water)

15.3

cosh

14.6

cosine defined

9.1

cosine, integral of

9.3 | 9.3

cot

11.2

counterclockwise

9.1

critical point

12.3

critical point theorem I

12.3

critical point theorem II

12.3

critical set

12.3

csc

11.2

D

decreasing function

5.3

derivative

0.1 | 0.1

derivative defined

10.3

derivative (fractional)

15.1

derivative (higher order)

15.1

derivative of absolute value

11.1

derivative of $\arccos$

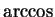
14.6

derivative of arccot

14.6

derivative of $\arcsin$

14.6

derivative of $\arctan$

14.6

derivative of $a^x$

14.6

derivative of $\cosh$

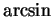
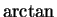
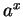
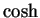
14.6

derivative of exponential

14.6

derivative of logarithm

11.1

derivative of order 0

15.1

derivative of powers

11.1

derivative of reciprocal

11.2

derivative of 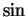$\sin$ and $\cos$

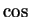
11.1

derivative of $\sinh$

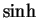
14.6

derivative of trigonometric functions

11.2

derivative of $x^r$

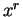
14.6

derivative (second)

15.1

derived function

0.1

Descartes, Rene (1596-1660)

10.1

difference of sets

1.

differential

0.1 | 0.1 | 11.1

differentiation

0.1

differentiation, logarithmic

11.3

Dirichlet,P.G.Lejenue(1805-1859)

8.3

discontinuous function

12.1

disjoint sets

5.1

disjoint (almost disjoint sets)

5.2

distance between numbers

6.1

distance between points

4.3

distributive law for points

4.1

divergent sequence

6.3

domain

3.3

double angle formulas

9.1

dummy index

1.

dummy variable

3.4 | 8.2 | 10.2

E

e

5.4

e (numerical calculatioin of)

6.7

ellipse (area of)

8.5

Emperor Yu(c. 21st century B.C.)

4.3

end points of interval

1.

entertainment $\lim \{n^{1\over n} \}$

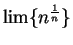
6.7

entertainment (Calculation of sines)

9.1

entertainment (Discontinuous derivative problem)

15.3

entertainment (Falling bodies problem)

10.1

entertainment (Archimedes sine integral)

9.3

entertainment (Calculate $\ln (2)$ )

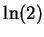5.4

entertainment (Composition problem)

11.3

entertainment (Area of a triangle)

5.3

entertainment (Square root problem)

0.3

entertainment (Calculate $e$)

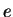5.4

entertainment (Pine Tree problem)

2.4

entertainment (Snowflake problem)

2.6

entertainment (Bernoulli's problem)

2.2

entertainment (Calculation of $\pi$)

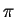0.3

entertainment (Congruence problem)

5.1

equal functions

3.3

equal propositions

3.1

equivalent proposition

3.1

error function

17.1

etymology of corollary

5.2

etymology of sine

9.1

Euclid ( fl. c. 300 B.C.)

1. | 2.4 | 10.1 | 10.3

Euler, Leonard (1707-1783)

3.3 | 6.3

Euler (summation notation)

3.4

even function

12.4

exponential function

14.3 | 14.4

exponential function (derivative of)

14.6

exponential function (properties of)

14.4

extreme point

12.3

extreme point (local)

12.3

extreme value property

12.3

F

fluxion

0.1 | 11.1

Fourier, Joseph (1768-1830)

8.1 | 15.1

fractional derivatives

15.1

function

0.1

function (bounded)

5.1

function (defined)

3.3

function (Euler's definition)

3.3

function (increasing)

5.3

functions equal

3.3

functions (operations on)

8.2

fundamental theorem of the calculus

0.1

fundamental theorem of calculus I

16.

fundamental theorem of calculus II

16.

Fundamental theorem of calculus (Leibniz statement of)

16.

G

Galileo (1564-1642)

10.1 | 10.1

geometric series

6.6

geometric series (finite)

2.4

Gougu

4.3

graph

3.3

graphs (area between)

8.6

gravity (acceleration due to)

15.2

H

half angle formulas

9.1

Hausdorff, Felix (1868-1942)

5.1

height of box

1.

Heine, Heinrich Eduard (1821-1881)

10.3

Heron (sometime between 250B.C and 150 A.D.)

13.3

higher order derivatives

15.1

hyperbolic functions

14.6

I

Ibn-al-Haitham (circa 1000 A.D.)

2.2

image of 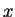$x$ under $f$

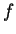
3.3

image of $f$

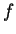
3.3

implies

3.1

increasing function

5.3

indefinite integral

9.4

induction

3.5

inequality rule for limits of functions

10.2

inequality rule for sequences

6.4

inequality theorem for integrals

8.2

inflection point

15.3

injective

14.3

inner snowflake

2.6

instantaneous velocity

10.3

integrable function

8.1

integral

8.1

integral (as area under a curve)

8.6

integral (Ei = exponential integral)

17.1

integral indefinite

9.4

integral of $\cos$

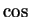
9.3 | 9.3

integral of $\sin$

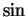
9.3 | 9.3

integral (Si = sine integral)

17.1

integral (change of scale in)

8.5

integration

0.1

integration by parts

17.3

integration by substitution

17.4

integration of rational functions

17.7

interior point

10.2

intermediate value property

14.1 | 14.1 | 14.1

intersection of sets

1. | 2.6

interval

1.

inverse function

14.3

inverse function theorem

14.5

K

Katyayana (c. 600 BC or 500BC??)

4.3

kinetic energy

15.2

Koch, Helga von(1870-1924)

2.6 | 12.2

L

l'Hôpital,Guillaume François (1661-1701)

6.3

Lagrange, Joseph Louis(1736-1813)

0.1

11.1

Leibniz, Gottfried (1646-1716)

0.1 | 0.1 | 0.1 | 3.3 | 8.1 | 8.2 | 10.1 | 11.1 | 13.3 | 15.1 | 16.

Leibniz (notation for sums)

3.4

Leibniz (proof of product rule)

11.2

length of arc

9.1

limit of a sequence

6.3

limit (one-sided)

13.1

limits (infinite)

13.1

lines

4.1

Liouville, Joseph (1809-1882)

15.1

ln(2) calculation

5.6

ln(a)

0.1

local maximum

12.3

local minimum

12.3

localization rule

11.1

logarithm

5.4 | 5.4 | 7.2

logarithm (derivative of)

11.1

logarithmic differentiation

11.3

M

Maple

5.6 | 17.1 | 17.6

Maple leftsum

5.6

Maple rightsum

5.6

Maple average

5.6

Maple calculation of $e$

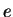
6.7

Maple mypi

9.2

Maple routine

9.2

Maple sinsq

9.2

Maple, approximate integration

5.6

Maple, symbolic antidifferentiation

17.1

Maple: integration

9.4

maximum (local)

12.3

maximum of function

12.3

mean value theorem

12.4

mean value theorem for integrals

16.

Mercator, Nicolaus (1620-1687)

5.5

mesh of partition

5.3

minimum (local)

12.3

minimum of function

12.3

monotonic function

5.3

monotonic (piecewise)

8.2

monotonicity of area

5.2 | B.

N

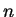$n$th root rule for sequences

6.4

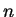$n$th power theorem

6.5

Napier, John(1550-1632)

5.4

Newton, Isaac(1642-1727)

0.1 | 0.1 | 10.3 | 11.1

Newton's law (F=ma)

0.1

nice function

16.

non-integrable function

8.3

normalization property of area

5.1

not (logical) operator

3.1

nowhere differentiable function

12.2

Nullsequence rule

6.4

number as area

1.

O

objects in a set

1.

odd function

12.4

open interval

1.

operations on functions

8.2

optical illusion

9.1

optimization problems

13.2

or (logical) operator

3.1

ordered pair

3.2

outer snowflake

2.6

P

pair (ordered pair)

3.2

parabola (area of)

2.1 | 2.3

parabolic segment (area of)

2.3

parallelogram

4.1

partition

5.3

partition regular

5.3

partition-sample sequence

8.2

Pascal, Blaise (1623-1662)

2.2

peicewise monotonic function

8.2

piecewise monotonic (example of non-piecewise monotonic function)

12.2

pi

0.1 | 0.3 | 0.3 | 5.6 | 8.5

pi, computer calculation

5.6

point in plane

1.

point of inflection

15.3

points (in $\mbox{{\bf R}}^2$)

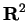4.1

points in a set

1.

points (addition of)

4.1

potential energy

15.2

power function

14.4

power (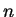$n$th power theorem)

6.5

power-sums (list of)

2.2

prerequisites

0.2

product rule for derivatives

11.2

product rule for limits

10.2

product rule for limits of functions

10.2

product rule for sequences

6.4

product (Cartesian)

3.2

proofs without words

2.2

proposition

3.1

proposition (set defined by)

3.2

proposition form

3.1

propositions (equality of)

3.1

propositions (equivalence of)

3.1

Ptolemy, Claudius (fl 127-151)

9.1

Pythagoras (f. 530-510 B.C.)

4.3

Pythagoreans

2.2

Q

quadratic formula

4.3

quotient rule for derivatives

11.2

quotient rule for limits

10.2

quotient rule for limits of functions

10.2

quotient rule for sequences

6.4

R

Ramanujan, Srinivasa (1887-1920)

0.3

rate of change

13.3

rational functions

17.7

rational number (definition)

1.

real number

0.1

reciprocal (derivative of)

11.2

reflection

2.3 | 4.2

reflection law for sin and cos

9.1

reflection theorem

14.3

regular partition

5.3

Rhind Papyrus

0.3

Riemann sum

7.1

Riemann, Bernhard (1826-1866)

8.1

right triangle

5.3

rituals for integration

17.4 | 17.4 | 17.5 | 17.6 | 17.6

Rolle, Michel (1652-1719)

12.4

Rolle's theorem

12.4

rotation

4.2

ruler function

8.4

S

Saint-Vincent, Grégoire de, (1584-1667)

6.6

sample

7.1

Sarasa, Alfons Anton de (1618-1667)

5.4

schizophrenia

3.1

sec$(x)$

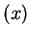
11.2

sector (circular)

17.5

segment

4.2

segments

4.1

sequence

3.3

sequence (constant sequence rule)

6.4

sequence (convergent)

6.3 | 6.3

sequence (divergent)

6.3

sequence (null sequence rule)

6.4

sequence (constant)

6.4

sequence (limit of)

6.3

sequence (product rule for)

6.4

sequence (sum rule for)

6.4

sequence (translate of)

6.4

sequence (translation rule for)

6.4

sequence (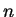$n$th root rule for)

6.4

sequences (inequality rule for)

6.4

sequences (quotient rule for)

6.4

set

1.

set (bounded)

5.1

sets defined by propositions

3.2

sine (definition)

9.1

sine (etymology of)

9.1

sine (integral of)

9.3 | 9.3

sine integral (Si)

17.1

sinh

14.6

snowflake

2.6 | 12.2

snowflake (area of)

2.6

spike function

8.2 | 8.2 | 10.2

square root problem

0.3

squeezing rule for limits of functions

10.2

squeezing rule for sequences

6.4

stretch

8.5

Stringham, Irving

5.4

subadditivity of area

5.2

subinterval of a partition

5.3

subset

1.

substitution in integrals

17.6

substitution (trigonometric)

17.5

sum rule for derivatives

11.2

sum rule for limits

10.2

sum rule for limits of functions

10.2

sum rule for sequences

6.4

sum theorem for derivatives

17.2

sum theorem for indefinite integrals

9.4

sum theorem for integrals

8.2

summation formula

2.2 | 2.2 | 2.2 | 2.2 | 2.2

surjective

14.3

symmetric set

12.4

symmetry invariance

5.1

symmetry of square

4.2

T

tangent

10.1 | 10.1 | 10.3

tan$(x)$

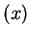
11.2

translate of a sequence

6.4

translate of set

4.2

translation invariance

5.1

translation rule for sequences

6.4

triangle inequality

6.1

triangle (area of)

5.3

triangle (right)

5.3

trick

6.5

trigonometric functions (definition)

9.1

trigonometric functions derivative of

11.1 | 11.2

trigonometric identities

9.1 | 9.1 | 9.1

trigonometric substitution

17.5

U

union of sets

1. | 2.6

uniqueness of inverses

14.3

Uniqueness theorem for convergence

6.3

unit circle

4.3

V

velocity

0.1 | 10.1 | 10.1

velocity (average)

10.3

velocity (instantaneous)

10.3

W

Weierstrass, Karl(1815-1897)

6.1 | 12.2

width of box

1.

work

0.1

Z

zero-area set

5.2 | 8.6

zeroth order derivative

15.1

Zu Chongzhi (429-500 A.D.)

0.3