



Next: 12. Extreme Values of
Up: 11. Calculation of Derivatives
Previous: 11.2 Some General Differentiation
Index
11.26
Definition (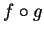 .)
.)
Let
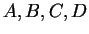
be sets and let
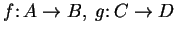
be functions.
The composition of

and

is the function
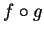
defined by:
i.e.,
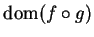
is the set of all points

such that
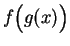
is defined. The rule for
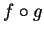
is
11.27
Example.
If
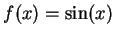
and
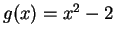
, then
and
Thus
So in this case
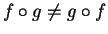
. Thus composition is not a commutative
operation.
If 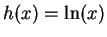 and
and 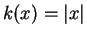 , then
, then
and
11.28
Exercise.
For each of the functions
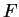
below,
find functions

and

such that
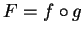
. Then find a formula
for
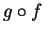
.
- a)
-
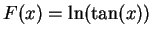 .
.
- b)
-
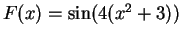 .
.
- c)
-
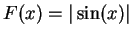 .
.
11.29
Exercise.
A
Let
Calculate formulas for
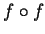
,
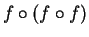
,
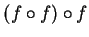
,
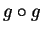
,
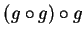
, and
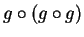
.
11.30
Entertainment (Composition problem.)
From the previous exercise you
should be able to find a subset
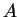
of
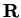
, and a function
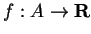
such that
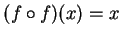
for all
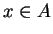
. You should also be able to find a subset
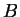
of
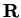
and a function
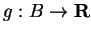
such that
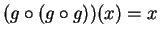
for all
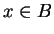
. Can you find a subset
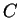
of
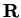
, and a function
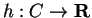
such that
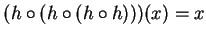
for
all
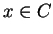
? One obvious example is the function

from the previous
example. To make the
problem more interesting, also add the condition that
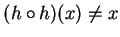
for some

in
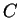
.
Before we prove the theorem we will give a few examples of how it is used:
11.32
Example.
Let
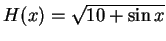
. Then
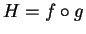
where
Hence
Let
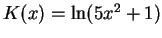 . Then
. Then 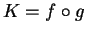 where
where
Hence
Usually I will not write out all of the details of a calculation like this.
I will just write:
Let
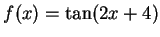 . Then
. Then
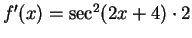 .
.
Proof of chain rule: Suppose  is differentiable at
is differentiable at  and
and  is differentiable at
is differentiable at
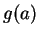 . Then
. Then
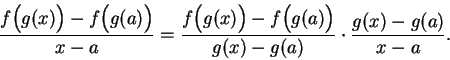 |
(11.33) |
Since  is differentiable at
is differentiable at  , we know that
, we know that
Hence the theorem will follow from (11.33), the definition of
derivative, and the
product rule for limits of functions, if we can show that
Since  is differentiable at
is differentiable at  , it follows from lemma 11.17
that
, it follows from lemma 11.17
that
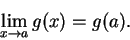 |
(11.34) |
Let 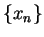 be a generic sequence in
be a generic sequence in
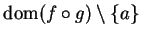 , such
that
, such
that
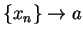 . Then by (11.34), we have
. Then by (11.34), we have
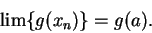 |
(11.35) |
Since
 is differentiable at
is differentiable at 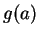 , we have
, we have
From this and (11.35) it follows that
Since this holds for a generic sequence 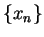 in
in
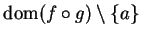 , we have
, we have
which is what we wanted to prove.
To complete the proof, I should show that  is an interior point of
is an interior point of
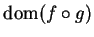 . This turns out to be rather tricky, so I will omit the proof.
. This turns out to be rather tricky, so I will omit the proof.
Remark: Our proof of the chain rule is not valid in all cases,
but it
is valid in all cases where you are likely to use it.
The proof fails in the case where every interval
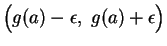 contains a point
contains a point 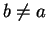 for which
for which
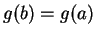 . (You should check the proof to see where this
assumption was made.) Constant functions
. (You should check the proof to see where this
assumption was made.) Constant functions  satisfy this condition, but if
satisfy this condition, but if  is
constant then
is
constant then 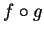 is also constant so the chain rule holds trivially in
this case. Since the proof in the general case is more technical than
illuminating, I am going to omit it. Can you find a non-constant function
is also constant so the chain rule holds trivially in
this case. Since the proof in the general case is more technical than
illuminating, I am going to omit it. Can you find a non-constant function  for which the proof fails?
for which the proof fails?
11.36
Example.
If

is differentiable at

, and
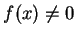
, then
Also
i.e.,
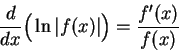 |
(11.37) |
I will use this relation frequently.
11.38
Example (Logarithmic differentiation.)
Let
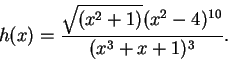 |
(11.39) |
The derivative of
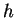
can be found by using the quotient rule and the product
rule
and the chain rule. I will use a trick here which is frequently useful. I
have
Now differentiate both sides of this equation using (
11.37) to get
Multiply both sides of the equation by
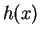
to get
This formula is not valid at points where
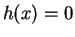
, because we took logarithms
in the calculation. Thus
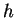
is differentiable at
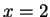
, but our formula for
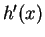
is not defined when
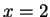
.
The process of calculating 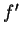 by first taking the logarithm of the
absolute value of
by first taking the logarithm of the
absolute value of  and then differentiating the result, is called logarithmic
differentiation.
and then differentiating the result, is called logarithmic
differentiation.
11.40
Exercise.
A
Let
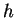
be the function defined in (
11.39) Show that
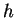
is differentiable at
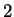
, and calculate
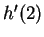
.




Next: 12. Extreme Values of
Up: 11. Calculation of Derivatives
Previous: 11.2 Some General Differentiation
Index
Ray Mayer
2007-09-07
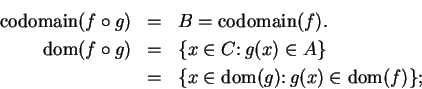
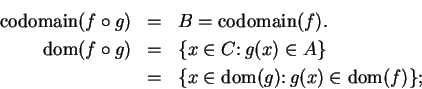
![]() and
and ![]() , then
, then
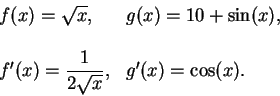
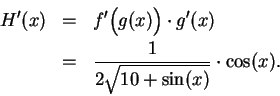
![]() . Then
. Then ![]() where
where
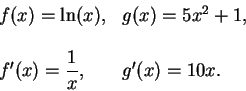
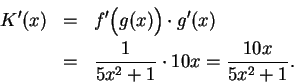
![]() . Then
. Then
![]() .
.
![]() is differentiable at
is differentiable at ![]() and
and ![]() is differentiable at
is differentiable at
![]() . Then
. Then
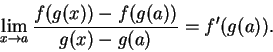
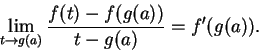
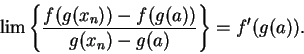
![]() contains a point
contains a point ![]() for which
for which
![]() . (You should check the proof to see where this
assumption was made.) Constant functions
. (You should check the proof to see where this
assumption was made.) Constant functions ![]() satisfy this condition, but if
satisfy this condition, but if ![]() is
constant then
is
constant then ![]() is also constant so the chain rule holds trivially in
this case. Since the proof in the general case is more technical than
illuminating, I am going to omit it. Can you find a non-constant function
is also constant so the chain rule holds trivially in
this case. Since the proof in the general case is more technical than
illuminating, I am going to omit it. Can you find a non-constant function ![]() for which the proof fails?
for which the proof fails?
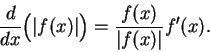
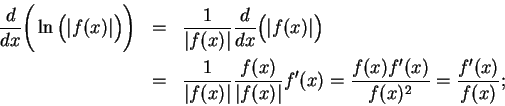
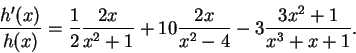
![\begin{displaymath}h^\prime (x)= {{\sqrt{x^2+1}(x^2-4)^{10}}\over {(x^3+x+1)^3}}...
...x^2+1}}+{{20x}\over {x^2-4}}-{{3(3x^2+1)}\over {x^3+x+1}}\Big].\end{displaymath}](img3074.gif)
![]() by first taking the logarithm of the
absolute value of
by first taking the logarithm of the
absolute value of ![]() and then differentiating the result, is called logarithmic
differentiation.
and then differentiating the result, is called logarithmic
differentiation.
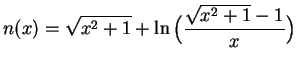 .
.
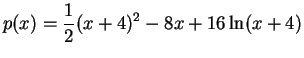 .
.
![$\displaystyle { q(x)={x\over 2}\Big[ \sin \Big(\ln (\vert 6x\vert)\Big)-\cos\Big(\ln
(\vert 6x\vert)\Big)\Big]}$](img3110.gif) .
.