



Next: B. Proofs of Some
Up: Math 111 Calculus I
Previous: Bibliography
Index
A. Hints and Answers
- Exercise 0.3:
- The Rhind value is
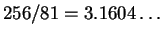
- Exercise 1.7:
- Look at the boundary.
- Exercise 1.10:
- If a set has no endpoints, then it contains all of its endpoints and none of its endpoints.
- Exercise 2.10:
-
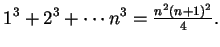
- Exercise 2.18:
- area
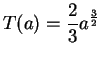 .
.
- Exercise 2.27:
-
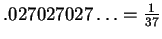 .
.
- Exercise 2.36:
- I let
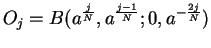 and
and
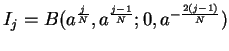 .
.
- Exercise 3.20:
- Recall
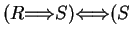 or not
or not 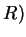 .
.
- Exercise 5.61:
-
![$S_1^{ab}[{1\over t}] = S_1^a[{1\over t}] \cup S_a^{ab}[{1\over t}]$](img4443.gif) . (Draw a picture.)
. (Draw a picture.)
- Exercise 5.80:
- Consider a partition with a fairly large number of points.
- Exercise 6.33:
- The assertion is false.
- Exercise 6.59:
- (part e) The limit is
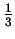 . It simplifies matters if you factor both the numerator and the denominator. The sequence in part g) is a translate of the sequence in part f).
. It simplifies matters if you factor both the numerator and the denominator. The sequence in part g) is a translate of the sequence in part f).
- Exercise 6.69:
- All four statements are false.
- Exercise 6.94:
- a)
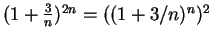 .
.
- Exercise 6.97:
-
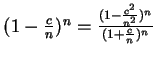 .
.
- Exercise 7.16:
- Take
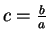 in lemma 7.13.
in lemma 7.13.
- Exercise 7.18:
-
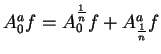 . Show that
. Show that
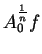 is small when
is small when  is large.
is large.
- Exercise 8.14:
-
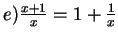 . Not all of these integrals exist.
. Not all of these integrals exist.
- Exercise 8.16:
- Show that
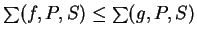 for every partition
for every partition 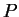 of
of ![$[a,b]$](img1071.gif) and every sample
and every sample 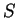 for
for 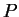 .
.
- Exercise 8.28:
 is the sum of an integrable function and a spike function.
is the sum of an integrable function and a spike function.
- Exercise 8.32:
 is not piecewise monotonic. It is easy to see that
is not piecewise monotonic. It is easy to see that  is integrable on
is integrable on ![$[1,2]$](img1125.gif) . If you can show it is integrable on
. If you can show it is integrable on ![$[0,1]$](img908.gif) then you are essentially done.
then you are essentially done.
- Exercise 8.34:
- b)
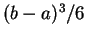 .
.
- Exercise 8.41:
- For any partition
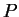 of
of ![$[0.1]$](img4453.gif) you can find a sample
you can find a sample 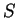 such that
such that
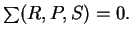
- Exercise 8.46:
- In equation 8.44, replace
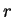 by
by 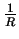 , , and replace
, , and replace  and
and 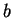 by
by 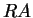 and
and 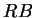 .
.
- Exercise 8.48:
-
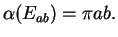
- Exercise 8.50:
- If
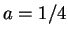 then both areas are approximately 3.1416
then both areas are approximately 3.1416
- Exercise 8.55:
- area =
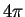 .
.
- Exercise 8.57:
- The areas are
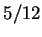 and
and 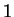 .
.
- Exercise 8.58:
- The area is
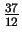 . Some fractions with large numerators may appear along the way.
. Some fractions with large numerators may appear along the way.
- Exercise 9.20:
- The last two formulas are obtained from the second by replacing
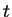 by
by 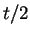 .
.
- Exercise 9.29:
- I used exercise 9.28 with
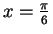 to find
to find
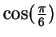 . You can also give a more geometric proof.
. You can also give a more geometric proof.
- Exercise 9.44:
- You will need to use (9.24).
- Exercise 9.48:
-
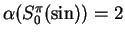 .
.
- Exercise 9.49:
- area
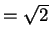 .
.
- Exercise 9.69:
-
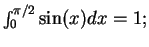
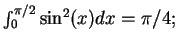
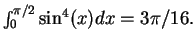
- Exercise 10.25:
-
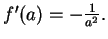
- Exercise 10.26:
- See example 10.9 and 9.26.
- Exercise 10.27:
-
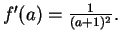
- Exercise 10.28:
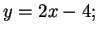
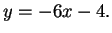
- Exercise 11.6:
- I used formula 9.25
- Exercise 11.15:
-
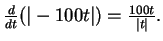
- Exercise 11.21:
- You can use the definition of derivative, or you can use the product rule and the reciprocal rule.
- Exercise 11.24:
-
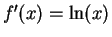 ,
,
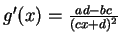 ,
,
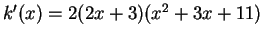
- Exercise 11.29:
-
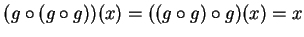 for
for
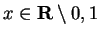 . If you said
. If you said
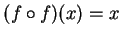 , calculate both sides when
, calculate both sides when 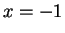 .
.
- Exercise 11.40:
- Use the definition of derivative.
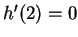 .
.
- Exercise 11.43:
-
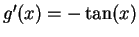 ,
,
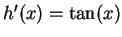 ,
,
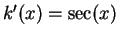 ,
,
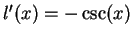 ,
,
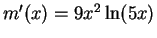 ,
,
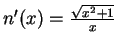 (It requires a lot of calculation to simplify
(It requires a lot of calculation to simplify 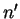 ),
),
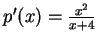 ,
,
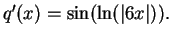
- Exercise 12.14:
- d) Such a function
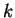 does exist.
does exist.
- Exercise 12.15:
- a) Use extreme value property.
- Exercise 12.27:
- Proof is like given proof of corollary 12.26.
- Exercise 12.31:
- Apply corollary 12.26 to
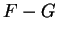 .
.
- Exercise 12.35:
- Yes.
- Exercise 12.36:
- You can apply the chain rule to the identity
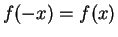 .
.
- Exercise 13.14:
- The function to minimize is
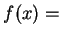 distance
distance
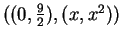 .
.
- Exercise 13.15:
- You may get a complicated equation of the form
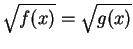 to solve. Square both sides and the equation should simplify.
to solve. Square both sides and the equation should simplify.
- Exercise 14.5:
- Apply the intermediate value property to
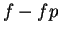 .
.
- Exercise 14.9:
- One of the zeros is in
![$[1,2]$](img1125.gif) .
.
- Exercise 14.10:
- I showed that if temp
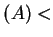 temp
temp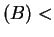 temp
temp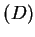 , then there is a point
, then there is a point 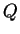 in
in 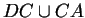 such that temp
such that temp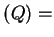 temp
temp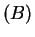 .
.
- Exercise 14.11:
- if temp
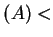 temp
temp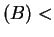 temp
temp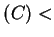 temp
temp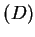 , find two points different from
, find two points different from 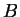 that have the same temperature as
that have the same temperature as 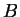 .
.
- Exercise 14.17:
- You may want to define some of these functions using more than one formula.
- Exercise 14.41:
- Use the extreme value property to get
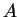 and
and 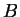 .
.
- Exercise 14.54:
-
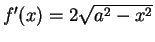 ;
;
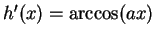 ;
;
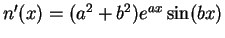 ;
;
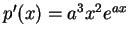 .
.
- Exercise 14.55:
- It is not true that
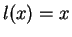 for all
for all  . Note that the image of
. Note that the image of 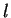 is
is
![$[-{\pi \over 2},{\pi\over 2}]$](img4509.gif) .
.
- Exercise 15.5:
-
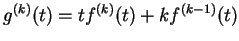 .
.
- Exercise 15.8:
- Use the antiderivative theorem twice.
- Exercise 15.9:
-
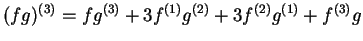 .
.
- Exercise 15.13:
- You will need to use a few trigonometric identities, including the reflection law (9.18).
- Exercise 15.22:
-
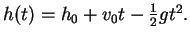
- Exercise 15.29:
- Use theorem 15.27 and corollary 12.26
- Exercise 16.2:
- You probably will not be able to find a ``single formula'' for this. My function has a local maximum at
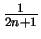 for all
for all
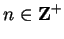 .
.
- Exercise 16.8:
- The result is known if
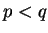 . To get the result when
. To get the result when 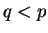 , apply 16.6 to
, apply 16.6 to  on
on ![$[q,p]$](img3892.gif) .
.
- Exercise 16.13:
- Not all of these integrals make sense.
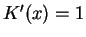 for all
for all
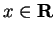 .
. 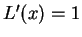 for
for
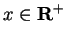 .
. 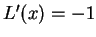 for
for
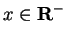 .
. 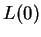 is not defined.
is not defined.
- Exercise 17.16:
- b)
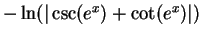 ; f)
; f)
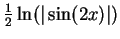 . i) Cf example 9.68i.j) You did this in exercise 9.69.
. i) Cf example 9.68i.j) You did this in exercise 9.69.
- Exercise 17.31:
- b)
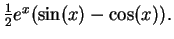 When you do the second integration by parts, be careful not to undo the first. c)
When you do the second integration by parts, be careful not to undo the first. c)
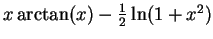 . Let
. Let 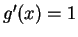 . d) and e) can be done easily without using integration by parts. f) If
. d) and e) can be done easily without using integration by parts. f) If 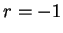 the answer is
the answer is
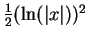 .
.
- Exercise 17.42:
- c) Let
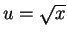 . You will need an integration by parts. d) Let
. You will need an integration by parts. d) Let 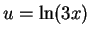 . e) Remember the definition of
. e) Remember the definition of 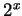 .
.
- Exercise 17.49:
- a)
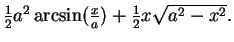 If you forget how to find
If you forget how to find
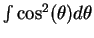 , review example 9.53. Also recall that
, review example 9.53. Also recall that
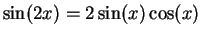 . b)
. b)
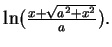 c) and d) do not require a trigonometric substitution.
c) and d) do not require a trigonometric substitution.
- Exercise 17.53:
- a)
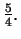 b)
b)
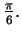 c)
c)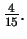
- Exercise 17.54:
-
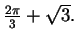
- Exercise 17.64:
- (g)
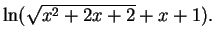 First complete the square, and then reduce the problem to
First complete the square, and then reduce the problem to
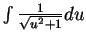 .
.




Next: B. Proofs of Some
Up: Math 111 Calculus I
Previous: Bibliography
Index
Ray Mayer
2007-09-07
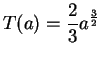 .
.
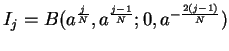 .
.
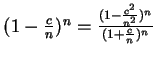 .
.
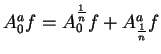 . Show that
. Show that
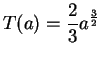 .
.
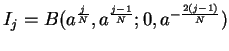 .
.
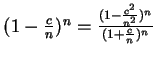 .
.
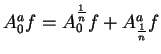 . Show that
. Show that