



Next: 15.3 Convexity
Up: 15. The Second Derivative
Previous: 15.1 Higher Order Derivatives
Index
15.16
Definition (Acceleration.)
If a particle
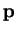
moves in
a straight line so that its position at time
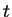
is
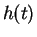
,
we have defined its velocity at time
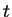
to be
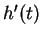
.
We now define its
acceleration at time
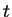
to be
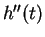
, so
that acceleration is the derivative of velocity. Thus if
a particle moves with a constant acceleration of
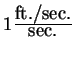
, then every second its velocity
increases by one ft./sec.
15.17
Example.
A mass on the end of a spring moves so that
its height at time
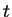
is
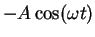
, where
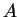
and
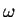
are positive numbers. If we denote its velocity at time
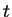
by
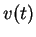
, and its
acceleration at time
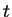
by
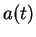
then
From this we see that the acceleration is always of opposite sign from
the position: when the mass is above the zero position it is being
accelerated downward, and when it is below its equilibrium position
it is being accelerated upward. Also we see that the magnitude of
the acceleration is largest when the velocity is
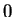
.
15.18
Definition (Acceleration due to gravity.)
If a particle
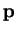
moves near the surface of the earth, acted on by no forces
except the force due to gravity, then
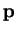
will move with a constant acceleration
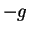
which is independent of the mass of
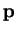
. The value of

is
We call
 the acceleration due to gravity
the acceleration due to gravity.
Actually, the value of

varies slightly over the surface of the earth,
so there is no exact value for

.
The law just described
applies in
situations when air resistance and buoyancy can be neglected. It describes the
motion of a falling rock well, but it does not describe a falling balloon.
Remark: When I solve applied problems, I
will usually omit all units (e.g. feet or seconds)
in my calculations, and will put them in only in the final answers.
15.19
Example.
A juggler
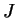
tosses a ball vertically upward from
a height of
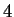
feet above the ground with a speed of
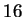
ft./sec. Let
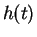
denote the height of the ball above the ground at time
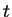
. We will set our
clock so that
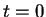
corresponds to the time of the toss:
We will suppose that while the ball is in the air, its motion is described
by a differentiable function of
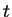
. We assume that
We know one function whose derivative is
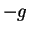
:
By the antiderivative theorem it follows that there is a constant
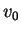
such that
Moreover we can calculate
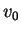
as follows:
Thus
We know a function whose derivative is
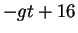
:
Thus there is a constant
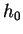
such that
To find
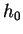
we set
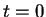
:
Thus
The ball will reach its maximum height when
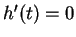
, i.e.
when
The maximum height reached by the ball is
so the ball rises to a maximum height of
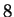
feet above the ground.
15.20
Example (Conservation of energy.)
Suppose that a particle
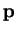
moves near the surface of the earth acted upon by no forces except the
force of gravity. Let
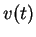
and
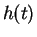
denote respectively its height
above the earth and its velocity at time
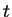
.
Then
so
Now
so we have
It follows that there is a constant
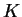
such that
or
If
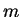
is the mass of the particle
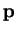
then
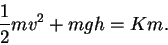 |
(15.21) |
The quantity
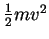
is called the
kinetic energy of
, and the
quantity
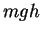
is called the
potential energy of
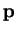
.
Equation (
15.21) states that as
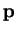
moves, the sum of its potential energy
end its kinetic energy remains constant.
15.22
Exercise.
A
A particle moves in a vertical line near the
surface of the earth, acted upon by
no forces except the force of gravity. At time
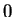
it is at height
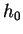
,
and has velocity
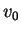
. Derive the formula for the height of the particle
at time
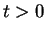
.
15.23
Exercise.
The acceleration due to gravity on the moon is
approximately
where

denotes the acceleration due to gravity on the earth. A juggler
on the moon wants to toss a ball vertically upward so that it rises
4 feet above its starting height. With what velocity should the ball leave
's hand?




Next: 15.3 Convexity
Up: 15. The Second Derivative
Previous: 15.1 Higher Order Derivatives
Index
Ray Mayer
2007-09-07
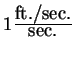 , then every second its velocity
increases by one ft./sec.
, then every second its velocity
increases by one ft./sec.
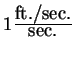 , then every second its velocity
increases by one ft./sec.
, then every second its velocity
increases by one ft./sec.