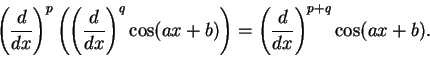Next: 15.2 Acceleration
Up: 15. The Second Derivative
Previous: 15. The Second Derivative
Index
15.1
Definition (Higher order derivatives.)
Let

be a function whose domain is a subset of
R. We define a function
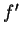
(called the
derivative of 
) by
and for all
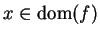
, the value of
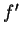
at

is the
derivative
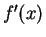
. We may also write
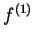
for
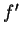
. Since
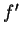
is itself a function, we can calculate its derivative: this
derivative is denoted by
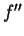
or
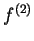
, and is called
the
second derivative of 
. For integers
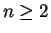
we define
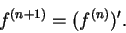 |
(15.2) |
and we call
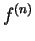
the
 th derivative of
th derivative of 
. We also
define
In Leibniz's notation
we write
so that equation (
15.2) becomes
If  and
and 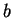 are real numbers, and
are real numbers, and  and
and  are functions
then from known properties of the derivative we can show that
are functions
then from known properties of the derivative we can show that
or
15.3
Examples.
If
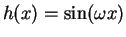
, where
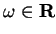
, then
It should now be apparent that
so that
If
then
If 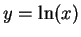 then
then
15.4
Exercise.
Calculate
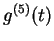
if
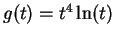
.
15.5
Exercise.
A
Let
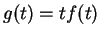
. Calculate
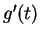
,
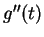
,
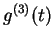
and
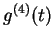
in terms
of
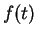
,
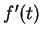
,
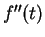
,
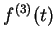
and
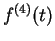
.
What do you think is the formula for
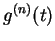
?
15.6
Exercise.
Find
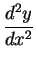
if
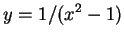
.
15.7
Exercise.
Find
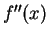
if
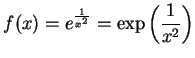
.
15.8
Exercise.
A
Suppose
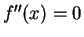
for all
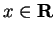
.
What can you say about

?
15.9
Exercise.
A
Let

and

be functions such that
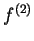
and
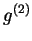
are defined on
all of
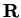
. Show that
Find a similar function for
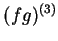
(assuming that
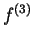
and
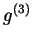
are defined.)
In Leibniz's calculus, 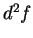 or
or 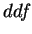 was actually
an infinitely
small quantity that was so much smaller than
was actually
an infinitely
small quantity that was so much smaller than 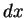 that the quotient
that the quotient
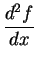 was zero, and
was zero, and
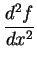 was obtained
by multiplying
was obtained
by multiplying 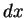 by itself and then dividing the result into
by itself and then dividing the result into 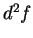 .
Leibniz also used notations like
.
Leibniz also used notations like
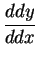 and
and
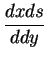 for which our modern notation has no counterparts.
Leibniz considered the problem of defining a meaning
for
for which our modern notation has no counterparts.
Leibniz considered the problem of defining a meaning
for
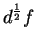 , but he did not make much progress
on this problem. Today there is considerable literature
on
fractional derivatives. A brief history of the subject
can be found in [36, ch I and ch VIII].
, but he did not make much progress
on this problem. Today there is considerable literature
on
fractional derivatives. A brief history of the subject
can be found in [36, ch I and ch VIII].
15.10
Exercise.
Let

be a real number.
Show that for
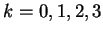
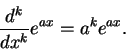 |
(15.11) |
After doing this it should be clear that
equation (
15.11), in fact holds for all
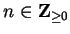
(this
can be proved by induction). Now suppose that
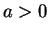
and we will
define
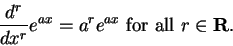 |
(15.12) |
Show that then for all
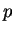
and
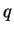
in
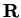
,
Find
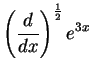
and
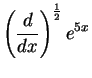
.
What do you think
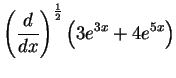
should be?
Equation (15.12) was the starting point from which Joseph Liouville (1809-1882) developed a theory of fractional calculus[36, pp 4-6].
15.13
Exercise.
A
Let

and
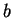
be real numbers. Show that for
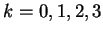
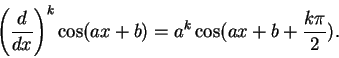 |
(15.14) |
After doing this exercise it should be clear that in fact
equation (
15.14) holds for all

(this can
be proved by induction).
Now suppose that
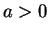
, and we will
define
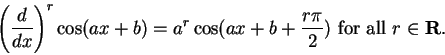 |
(15.15) |
Show that for all
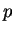
and
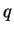
in
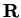
Equation (
15.15) was used as the starting point for a definition
of fractional derivatives for general functions,
by Joseph Fourier (1768-1830)[
36, page 3].




Next: 15.2 Acceleration
Up: 15. The Second Derivative
Previous: 15. The Second Derivative
Index
Ray Mayer
2007-09-07
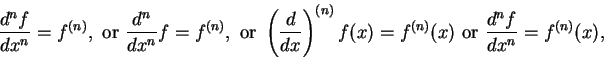
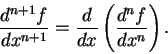
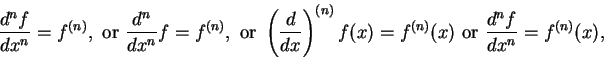
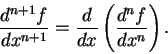
![]() and
and ![]() are real numbers, and
are real numbers, and ![]() and
and ![]() are functions
then from known properties of the derivative we can show that
are functions
then from known properties of the derivative we can show that
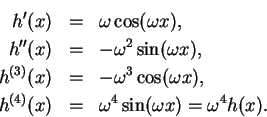
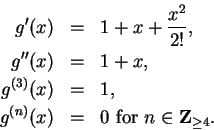
![]() then
then
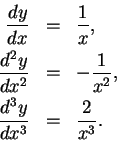
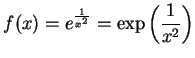 .
.
![]() or
or ![]() was actually
an infinitely
small quantity that was so much smaller than
was actually
an infinitely
small quantity that was so much smaller than ![]() that the quotient
that the quotient
![]() was zero, and
was zero, and
![]() was obtained
by multiplying
was obtained
by multiplying ![]() by itself and then dividing the result into
by itself and then dividing the result into ![]() .
Leibniz also used notations like
.
Leibniz also used notations like
![]() and
and
![]() for which our modern notation has no counterparts.
Leibniz considered the problem of defining a meaning
for
for which our modern notation has no counterparts.
Leibniz considered the problem of defining a meaning
for
![]() , but he did not make much progress
on this problem. Today there is considerable literature
on
fractional derivatives. A brief history of the subject
can be found in [36, ch I and ch VIII].
, but he did not make much progress
on this problem. Today there is considerable literature
on
fractional derivatives. A brief history of the subject
can be found in [36, ch I and ch VIII].
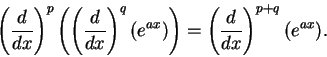
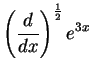 and
and
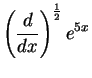 .
What do you think
.
What do you think
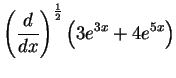 should be?
should be?