


Next: 17.3 Integration by Parts
Up: 17. Antidifferentiation Techniques
Previous: 17.1 The Antidifferentiation Problem
Index
Every differentiation formula gives rise to an antidifferentiation formula.
We review here a list of formulas that you should know.
In each case you should verify the formula by differentiating the right side.
You should know these formulas backward and forward.
17.7
Exercise.
Verify that
and
It follows from the previous exercise that
and
You should add these two formulas to the list of antiderivatives to be
memorized.
Proof:
The meaning of this statement is that if 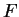 is an antiderivative for
is an antiderivative for 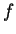 and
and 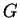 is an antiderivative for
is an antiderivative for 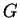 , then
, then 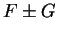 is an antiderivative for
is an antiderivative for
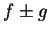 , and
, and 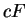 is an antiderivative for
is an antiderivative for 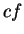 . The
warning about ambiguous notation
for indefinite integrals given in chapter 9
applies also to antiderivatives.
. The
warning about ambiguous notation
for indefinite integrals given in chapter 9
applies also to antiderivatives.
Let 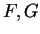 be antiderivatives for
be antiderivatives for 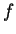 and
and 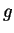 respectively
on
respectively
on ![$[a,b]$](img1071.gif) . Then
. Then 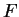 and
and 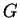 are continuous on
are continuous on ![$[a,b]$](img1071.gif) , and
, and
on 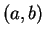 . Hence
. Hence 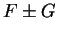 are continuous on
are continuous on ![$[a,b]$](img1071.gif) , and
, and
on 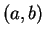 ,
and hence
,
and hence
Also 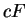 is continuous on
is continuous on ![$[a,b]$](img1071.gif) , and
, and
on 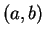 ,
so that
,
so that
17.10
Example.
We will calculate
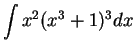
.
I will try to bring this
integral into the form
It appears reasonable to take
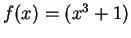
, and then
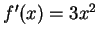
.
The
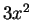
doesn't quite appear in the integral, but I can
get it where I need it by multiplying by a constant, and using (
17.9):
17.11
Example.
We will calculate
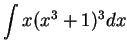
.
This problem is more complicated than the last one.
Here I still want to take
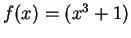 , but I cannot
get the ``
, but I cannot
get the ``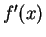 '' that I need. I will multiply out
'' that I need. I will multiply out 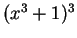
17.12
Example.
We will calculate
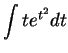
.
Since
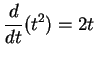
we get
17.13
Example.
We will consider
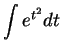
.
Although this problem looks similar to the one we just did,
it can be shown that no function built
up from the functions we have studied by algebraic operations is an
antiderivative for 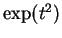 . So we will not find the
desired antiderivative. (But by the fundamental theorem of the calculus
we know that
. So we will not find the
desired antiderivative. (But by the fundamental theorem of the calculus
we know that 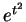 has an antiderivative.)
has an antiderivative.)
17.14
Example.
We will calculate
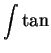
.
17.15
Example.
We will calculate
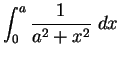
.
The integrand
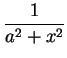 looks enough like
looks enough like
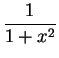 that I will try to get an
that I will try to get an 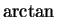 from this integral.
from this integral.
Now
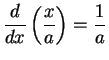
,
so
Thus we have found an antiderivative for
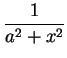
.
Hence



Next: 17.3 Integration by Parts
Up: 17. Antidifferentiation Techniques
Previous: 17.1 The Antidifferentiation Problem
Index
Ray Mayer
2007-09-07
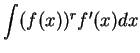
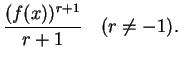
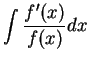
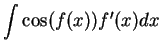
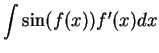
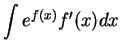
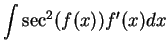
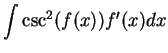
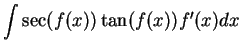
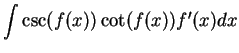
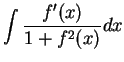
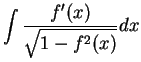
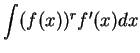
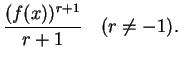
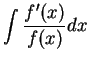
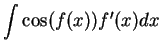
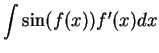
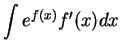
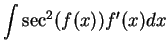
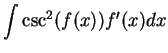
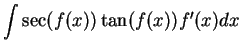
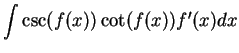
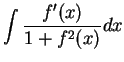
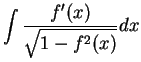
![]() be antiderivatives for
be antiderivatives for ![]() and
and ![]() respectively
on
respectively
on ![]() . Then
. Then ![]() and
and ![]() are continuous on
are continuous on ![]() , and
, and
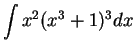 .
.
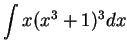 .
.
![]() , but I cannot
get the ``
, but I cannot
get the ``![]() '' that I need. I will multiply out
'' that I need. I will multiply out ![]()
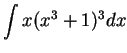
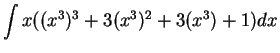
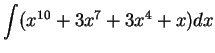
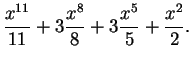
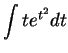 .
.
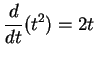 we get
we get
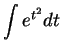 .
.
![]() . So we will not find the
desired antiderivative. (But by the fundamental theorem of the calculus
we know that
. So we will not find the
desired antiderivative. (But by the fundamental theorem of the calculus
we know that ![]() has an antiderivative.)
has an antiderivative.)
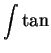 .
.
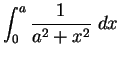 .
.
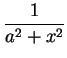 looks enough like
looks enough like
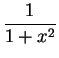 that I will try to get an
that I will try to get an ![]() from this integral.
from this integral.
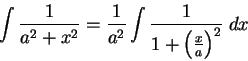
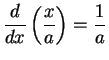 ,
so
,
so
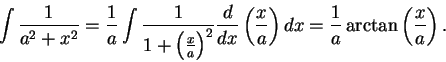
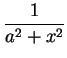 .
Hence
.
Hence