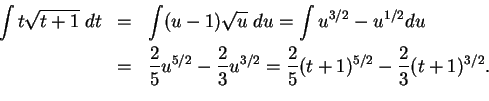Next: 17.5 Trigonometric Substitution
Up: 17. Antidifferentiation Techniques
Previous: 17.3 Integration by Parts
Index
17.4 Integration by Substitution
We will now use the chain rule to find some antiderivatives. Let  be a real
valued function that is continuous on some interval
be a real
valued function that is continuous on some interval 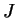 and differentiable on
the
interior of
and differentiable on
the
interior of 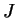 , and let
, and let  be a function such that
be a function such that  has an antiderivative
has an antiderivative
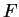 on some interval
on some interval 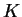 . We will suppose that
. We will suppose that 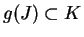 and
and
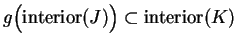 . It then follows that
. It then follows that 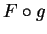 is continuous on
is continuous on
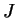 and differentiable on
and differentiable on
 , and
, and
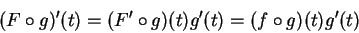 |
(17.32) |
for all 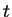 in the interior of
in the interior of 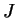 ; i.e.,
; i.e., 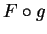 is an antiderivative for
is an antiderivative for
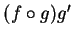 on
on 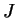 . Thus
. Thus
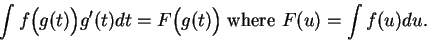 |
(17.33) |
There is a standard ritual
for using (17.33) to find
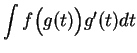 when an antiderivative
when an antiderivative 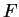 can be found for
can be found for  . We write:
. We write:
Let 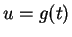 . Then
. Then 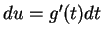 (or
(or
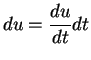 ), so
), so
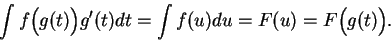 |
(17.34) |
In the first equality of (17.34) we replace 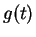 by
by 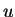 and
and 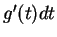 by
by
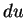 , and in the last step we replace
, and in the last step we replace 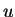 by
by 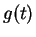 . Since we have never
assigned
any meaning to ``
. Since we have never
assigned
any meaning to `` 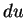 " or ``
" or `` 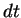 ",
we should think of (17.34)
just as a mnemonic device for remembering (17.33).
",
we should think of (17.34)
just as a mnemonic device for remembering (17.33).
17.35
Example.
Find
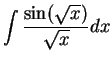
.
Let 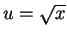 . Then
. Then
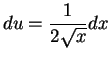 , so
, so
Suppose we want to find
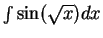 . If we had a
. If we had a 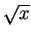 in the
denominator, this would be a simple problem. (In fact we just considered this
problem in the previous example.) We will now discuss a method of introducing
the missing
in the
denominator, this would be a simple problem. (In fact we just considered this
problem in the previous example.) We will now discuss a method of introducing
the missing 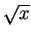 .
.
Suppose  is a function on an interval
is a function on an interval 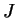 such that
such that 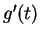 is never zero on
the interior of
is never zero on
the interior of 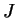 , and suppose that
, and suppose that 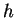 is an inverse function for
is an inverse function for  . Then
. Then
for all  in the interior of
in the interior of 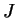 , so
, so
We now apply the ritual (17.34):
Let 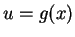 . Then
. Then 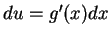 , so
, so
If we can find an antiderivative 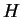 for
for 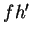 , then
, then
We have shown that if 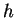 is an inverse function for
is an inverse function for  , then
, then
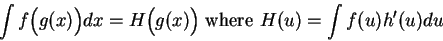 |
(17.36) |
There is a ritual
associated with this result also. To find
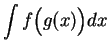 :
:
Let 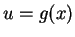 . Then
. Then 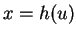 so
so 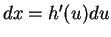 .
.
Hence
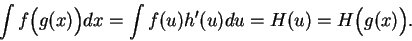 |
(17.37) |
17.38
Example.
To find
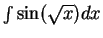
.
Let 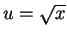 . Then
. Then 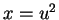 so
so 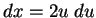 .
.
Thus
We can now use integration by parts to find
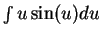
.
Let
Then
Hence
17.39
Example.
To find
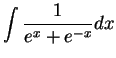
.
Let 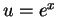 . Then
. Then 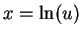 so
so
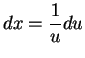 .
.
17.40
Example.
To find
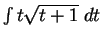
.
Let 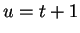 . Then
. Then 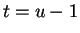 so
so 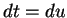 .
.
Hence
17.41
Example.
To find
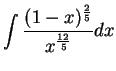
.
Let
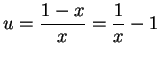
. Then
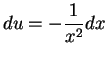
,
and
Thus
17.42
Exercise.
A
Find the following antiderivatives:
- a)
-
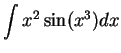 .
.
- b)
-
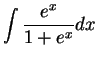 .
.
- c)
-
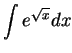 .
.
- d)
-
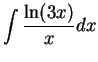 .
.
- e)
-
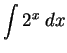 .
.
- f)
-
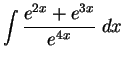 .
.
- g)
-
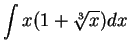 .
.




Next: 17.5 Trigonometric Substitution
Up: 17. Antidifferentiation Techniques
Previous: 17.3 Integration by Parts
Index
Ray Mayer
2007-09-07
![]() be a real
valued function that is continuous on some interval
be a real
valued function that is continuous on some interval ![]() and differentiable on
the
interior of
and differentiable on
the
interior of ![]() , and let
, and let ![]() be a function such that
be a function such that ![]() has an antiderivative
has an antiderivative
![]() on some interval
on some interval ![]() . We will suppose that
. We will suppose that ![]() and
and
![]() . It then follows that
. It then follows that ![]() is continuous on
is continuous on
![]() and differentiable on
and differentiable on
![]() , and
, and
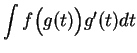 when an antiderivative
when an antiderivative ![]() can be found for
can be found for ![]() . We write:
. We write:
![]() . Then
. Then ![]() (or
(or
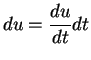 ), so
), so
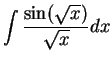 .
.
![]() . Then
. Then
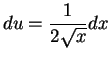 , so
, so
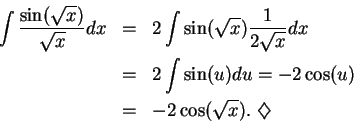
![]() is a function on an interval
is a function on an interval ![]() such that
such that ![]() is never zero on
the interior of
is never zero on
the interior of ![]() , and suppose that
, and suppose that ![]() is an inverse function for
is an inverse function for ![]() . Then
. Then
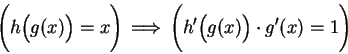
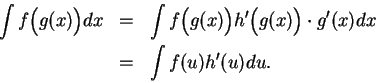
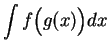 :
:
![]() . Then
. Then ![]() so
so ![]() .
.
![]() . Then
. Then ![]() so
so ![]() .
.
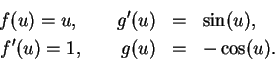
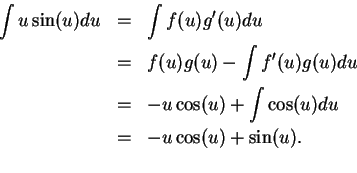
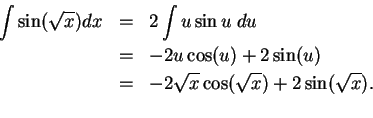
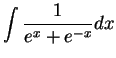 .
.
![]() . Then
. Then ![]() so
so
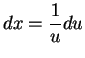 .
.
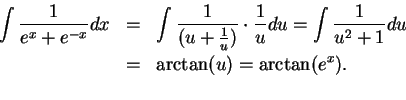
![]() . Then
. Then ![]() so
so ![]() .
.