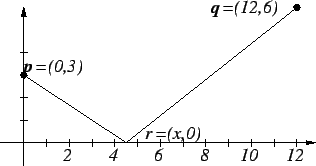Next: 13.3 Rates of Change
Up: 13. Applications
Previous: 13.1 Curve Sketching
Index
13.8
Example.
A stick of length
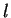
is to be broken into four pieces of length
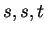
and
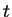
and the pieces are to be assembled to make a rectangle. How should
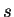
and
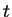
be chosen if the area of the rectangle is to be as large as possible? What
is
the area of this largest rectangle? Before doing the problem you should guess
the
answer. Your guess will probably be correct.
Let 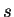 be the length of one side of the rectangle. Then
be the length of one side of the rectangle. Then 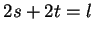 so
so
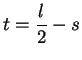 ; i.e.,
; i.e., 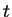 is a function of
is a function of 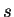 . Let
. Let 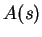 be the area
of a
rectangle with side
be the area
of a
rectangle with side 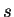 . Then
. Then
I include the endpoints for convenience; i.e., I consider rectangles with zero
area to be admissible candidates for my answer. These clearly correspond to
minimum area. Now
so
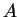
has only one critical point, namely
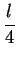
, and
Since
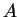
is continuous on
![$\displaystyle {\Big[
0,{l\over
2}\Big]}$](img3334.gif)
we know that
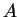
has a maximum and a minimum, and since
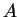
is
differentiable on
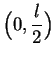
the extreme points are a
subset
of
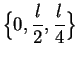
. Since
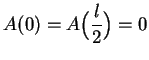
the maximal area is
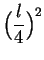
; i.e., the
maximal
rectangle is a square. (As you probably guessed.)
This problem is solved by Euclid in completely geometrical terms [17, vol 1
page
382].
Euclid's proof when transformed from geometry to algebra becomes the following.
Suppose in our problem  , say
, say  . Since
. Since
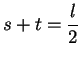 , it
follows that
, it
follows that
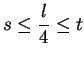 (if
(if  and
and  were both less than
were both less than
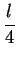 , we'd get a contradiction, and if they were both greater than
, we'd get a contradiction, and if they were both greater than
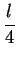 , we'd get a contradiction). Let
, we'd get a contradiction). Let 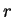 be defined by
be defined by
Then
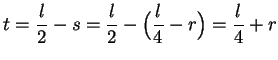
so
Hence, if
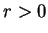
,
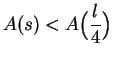
and to get a maximum we
must have
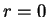
and
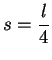
. This proof requires knowing the
answer ahead
of time (but you probably were able to guess it). In any case, Euclid's
argument
is special, whereas our calculus proof applies in many situations.
Quadratic polynomials can be minimized (or maximized) without calculus by
completing the square. For example, we have
From this we can easily see that
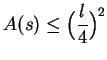
for all
and equality holds only if
. This technique applies only
to quadratic polynomials.
13.9
Example.
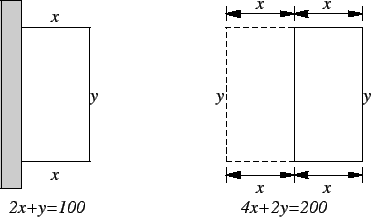
Suppose I have 100 ft. of fence, and I want to fence off 3 sides of a
rectangular garden, the fourth side of which lies against a wall and
requires no fence (see the figure).
What should the sides of the
garden be if the area is to be as large as possible?
This is a straightforward problem, and in the next exercise you will do it by
using calculus. Here I want to indicate how to do the problem
without calculation.
Imagine that the wall is a mirror, and that my fence is reflected in the wall.
When
I maximize the area of a garden with a rectangle of sides

and
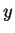
, then I
have
maximized the area of a rectangle bounded by 200 feet of fence (on four sides)
with
sides
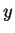
and
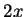
. From the previous problem the answer to this problem is a
square with
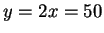
. Hence, the answer to my original question is
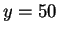
,
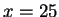
. Often optimization problems have solutions that can be guessed on the
basis of symmetry. You should try to guess answers to these problems before
doing
the calculations.
13.10
Exercise.
Verify my solution in the previous example by using calculus and by
completing the square.
13.11
Example.
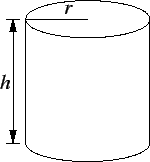
I want to design a cylindrical can of radius
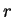
and height
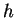
with a
volume of
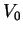
cubic feet (
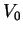
is a constant). How should I choose
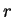
and
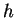
if the amount of tin in the can is to be minimum?
Here I don't see any obvious guess to make for the answer.
I have
so
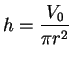
. Let
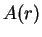
be the surface area of the can
of
radius
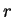
. Then
The domain of
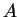
is
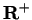
. It is clear that
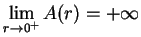
, and
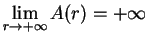
. Now
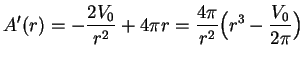
. The only critical point for
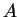
is
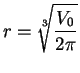
(call this number
). Then
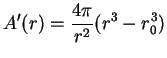
. We see that
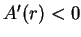
for
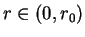
and
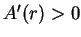
for
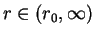
so
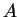
is decreasing on
![$(0,r_0]$](img3371.gif)
and
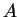
is increasing on
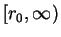
and thus
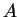
has a minimum
at
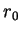
. The value of
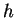
corresponding to
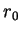
is
Thus the height of my can is equal to its diameter; i.e., the can will exactly
fit
into a cubical box.
In the following four exercises see if you can make a reasonable guess to the
solutions before you use calculus to find them.
13.12
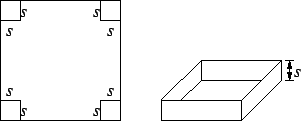
Exercise.
A box (without a lid) is to be made by cutting 4 squares of side
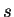
from
the
corners of a
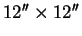
square, and folding up the corners as indicated in the
figure.
How should
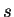
be chosen to make the volume of the box as large as
possible?
13.13
Exercise.
A rectangular box with a square bottom and no lid is to be built having a
volume of 256 cubic inches. What should the dimensions be, if the total
surface area of the
box
is to be as small as possible?
13.14
Exercise.
A
Find the point(s) on the parabola whose equation is
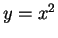
that are
nearest
to the point
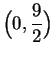
.
13.15
Exercise.
A
Let
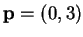
and let
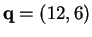
. Find the point(s)
r on
the

-axis so that path from
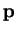
to
r to
q is as short as possible;
i.e.,
such that length([
p
r])
length([
r
q]) is as short as possible.
You don't need to prove that the critical point(s) you find are actually
minimum points.




Next: 13.3 Rates of Change
Up: 13. Applications
Previous: 13.1 Curve Sketching
Index
Ray Mayer
2007-09-07
![]() be the length of one side of the rectangle. Then
be the length of one side of the rectangle. Then ![]() so
so
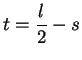 ; i.e.,
; i.e., ![]() is a function of
is a function of ![]() . Let
. Let ![]() be the area
of a
rectangle with side
be the area
of a
rectangle with side ![]() . Then
. Then
![$\displaystyle {\Big[
0,{l\over
2}\Big]}$](img3334.gif) we know that
we know that 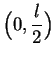 the extreme points are a
subset
of
the extreme points are a
subset
of
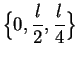 . Since
. Since
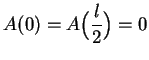 the maximal area is
the maximal area is
![]() , say
, say ![]() . Since
. Since
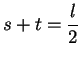 , it
follows that
, it
follows that
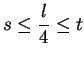 (if
(if ![]() and
and ![]() were both less than
were both less than
![]() , we'd get a contradiction, and if they were both greater than
, we'd get a contradiction, and if they were both greater than
![]() , we'd get a contradiction). Let
, we'd get a contradiction). Let ![]() be defined by
be defined by
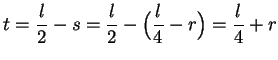 so
so
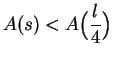 and to get a maximum we
must have
and to get a maximum we
must have 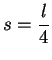 . This proof requires knowing the
answer ahead
of time (but you probably were able to guess it). In any case, Euclid's
argument
is special, whereas our calculus proof applies in many situations.
. This proof requires knowing the
answer ahead
of time (but you probably were able to guess it). In any case, Euclid's
argument
is special, whereas our calculus proof applies in many situations.
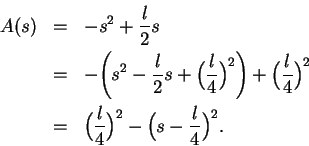
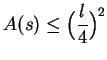 for all
for all
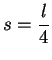 . This technique applies only
to quadratic polynomials.
. This technique applies only
to quadratic polynomials.
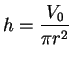 . Let
. Let 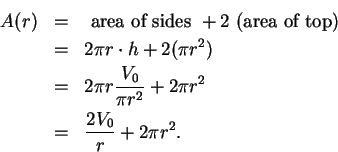
 . The only critical point for
. The only critical point for 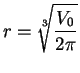 (call this number
(call this number 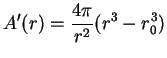 . We see that
. We see that
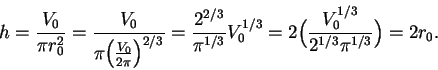
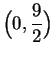 .
.