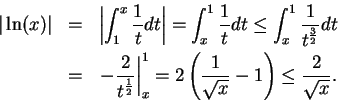Next: 13.2 Optimization Problems.
Up: 13. Applications
Previous: 13. Applications
Index
13.1
Example.
Let
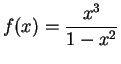
. Here
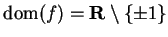
and

is an odd function. We have
From this we see that the critical set for

is
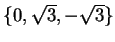
.
We can determine the sign of
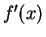
by looking at the signs of its
factors:
Since

is odd, I will consider only points where
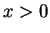
.
Thus

is strictly increasing on
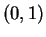
and on
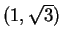
, and

is
strictly decreasing on
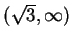
. Also
We see that
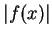
is unbounded on any interval
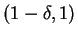
or
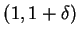
,
since the numerator of the fraction is near to
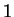
, and the denominator is near
to
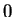
on these intervals. Also
so
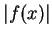
is large when

is large. (
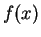
is the product of

and a
number
near to
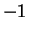
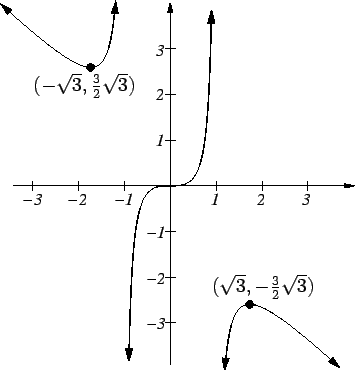
.) Using this information we can make a reasonable sketch of the
graph
of

.
Here  has a local maximum at
has a local maximum at 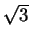 and a local minimum at
and a local minimum at 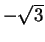 .
It has no global extreme points.
.
It has no global extreme points.
13.2
Definition (Infinite limits.)
Let
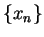
be a real sequence. We say
if for every
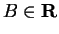
there is an
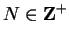
such that for all
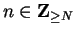
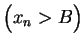
.
We say
if for every
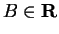
there is an
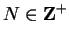
such that for all
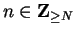
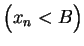
.
Let

be a real valued function such that
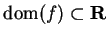
, and let
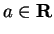
. We say
if
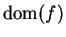
contains an interval
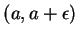
and for every sequence
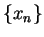
in
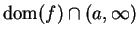
We say
if
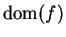
contains an interval
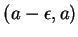
and for every sequence
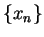
in
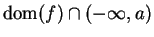
Similar definitions can be made for
We say
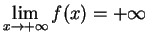
if
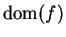
contains some
interval
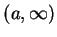
and for every sequence
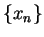
in
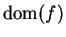
Similarly if
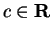
we can define
13.3
Example.
If

is the function in the previous example (i.e.
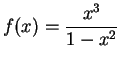
) then
and
Also,
and
The situation here is very similar to the situation in the case of ordinary
limits,
and we will proceed without writing out detailed justifications.
13.4
Exercise.
Write out definitions for
13.5
Exercise.
Find one function

satisfying all of the following conditions:
13.6
Example.
Let
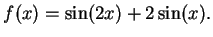
Then
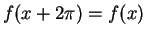
for all
,
so I will restrict my attention to the interval
![$[-\pi ,\pi ]$](img3301.gif)
.
Also

is an odd function, so I will further restrict my attention to the
interval
![$[0,\pi]$](img2542.gif)
. Now
Hence

is a critical point for

if and only if
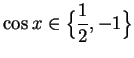
. The critical points of

in
![$[0,\pi]$](img2542.gif)
are thus
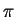
and
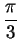
, and the critical points in
![$[-\pi ,\pi ]$](img3301.gif)
are
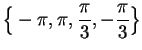
. Now
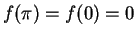
and
and
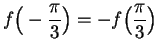
. Also note
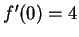
. Since

is continuous on
![$[-\pi ,\pi ]$](img3301.gif)
, we know that

has a
maximum and a minimum on this interval, and since
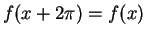
for all
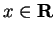
,
the maximum
(or minimum)
of

on
![$[-\pi ,\pi ]$](img3301.gif)
will be a global maximum (or minimum) for

. Since

is
differentiable everywhere, the extreme points are critical points and from our
calculations

has a maximum at
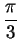
and a minimum at
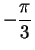
. I will now determine the sign of
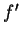
on
![$[0,\pi]$](img2542.gif)
:
Thus

is strictly increasing on
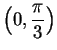
and

is
strictly decreasing on
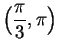
. We can now make a
reasonable sketch for the graph of

.
13.7
Exercise.
Sketch and discuss the graphs of the following functions. Mention all
critical points and determine whether each critical point is a local or global
maximum or minimum.
- a)
-
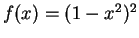 .
.
- b)
-
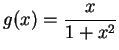 .
.
- c)
-
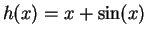 .
.
- d)
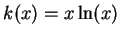 .
.
(The following remark may be helpful for
determining
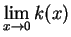
. If
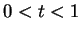
, then
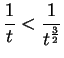
. Hence if
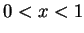
, then
Thus,




Next: 13.2 Optimization Problems.
Up: 13. Applications
Previous: 13. Applications
Index
Ray Mayer
2007-09-07
 . Here
. Here
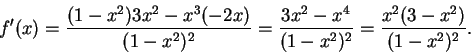
![\begin{displaymath}\begin{array}{\vert c\vert c\vert c\vert c\vert}\hline
& 0<x<...
...ex] \hline
f^\prime (x) & + & + & - [2ex] \hline
\end{array}\end{displaymath}](img3265.gif)
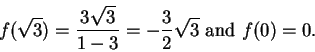
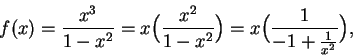
![]() has a local maximum at
has a local maximum at ![]() and a local minimum at
and a local minimum at ![]() .
It has no global extreme points.
.
It has no global extreme points.
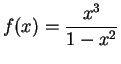 . Here
. Here
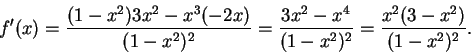
![\begin{displaymath}\begin{array}{\vert c\vert c\vert c\vert c\vert}\hline
& 0<x<...
...ex] \hline
f^\prime (x) & + & + & - [2ex] \hline
\end{array}\end{displaymath}](img3265.gif)
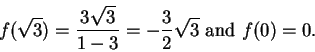
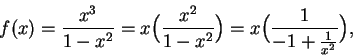

![]() has a local maximum at
has a local maximum at ![]() and a local minimum at
and a local minimum at ![]() .
It has no global extreme points.
.
It has no global extreme points.
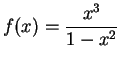 ) then
) then
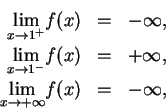
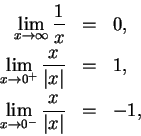
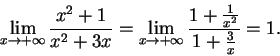
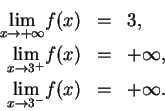
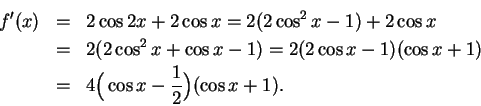
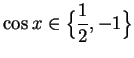 . The critical points of
. The critical points of 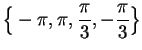 . Now
. Now 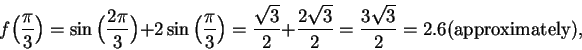
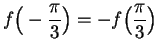 . Also note
. Also note
![\begin{displaymath}\begin{array}{\vert l\vert l\vert l\vert}\hline
& 0<x<{\pi\ov...
... [2ex] \hline
f^\prime (x) & + & - [2ex] \hline
\end{array}\end{displaymath}](img3312.gif)
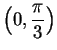 and
and 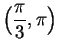 . We can now make a
reasonable sketch for the graph of
. We can now make a
reasonable sketch for the graph of 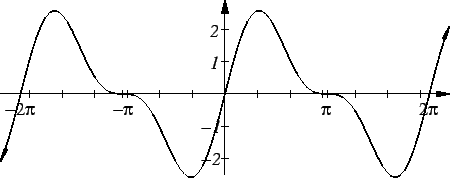
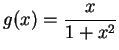 .
.
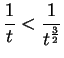 . Hence if
. Hence if