



Next: 11.2 Some General Differentiation
Up: 11. Calculation of Derivatives
Previous: 11. Calculation of Derivatives
Index
Proof: First consider the case 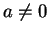 . For all
. For all  in
domain
in
domain
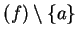 we have
we have
Let 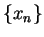 be a generic sequence in domain
be a generic sequence in domain
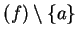 such that
such that
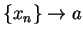 . Let
. Let
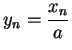 . Then
. Then 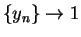 and hence
by theorem 7.10 we have
and hence
by theorem 7.10 we have
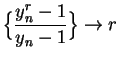 and hence
and hence
This proves the theorem in the case 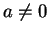 . If
. If 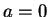 then
then
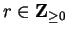 (since for other values of
(since for other values of 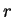 ,
, 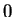 is not an interior point of domain
is not an interior point of domain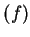 ).
In
this case
).
In
this case
Hence
Thus in all cases the formula
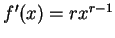 holds.
holds. 
11.2
Corollary (Of the proof of theorem 11.1) For all
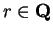 ,
,
Proof: If 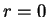 the result is clear, so we assume
the result is clear, so we assume 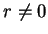 . For all
. For all
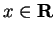 and all
and all
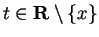 , we have
, we have
(Here I've used an identity from theorem 9.21.) Let 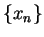 be a
generic sequence in
be a
generic sequence in
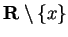 such that
such that 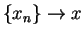 . Let
. Let
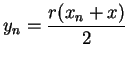 and let
and let
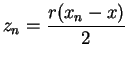 . Then
. Then
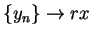 so by lemma 9.34 we have
so by lemma 9.34 we have
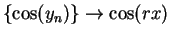 . Also
. Also
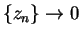 , and
, and
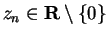 for all
for all
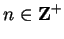 ,
so by (9.38),
,
so by (9.38),
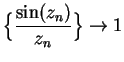 . Hence
. Hence
and this proves formula (11.4). 
The proof of (11.5) is similar.
11.6
Exercise.
A
Prove that if
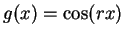
, then
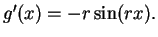
11.7
Theorem (Derivative of the logarithm.) The logarithm function is differentiable on
 , and
, and
Proof: Let
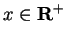 , and let
, and let
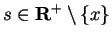 . Then
. Then
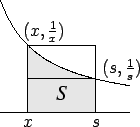
Case 1: If 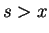 then
then
![$\displaystyle {A_x^s \Big[ {1\over t}\Big]}$](img2877.gif) represents the area
of the shaded region
represents the area
of the shaded region 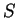 in the figure.
in the figure.
We have
so by monotonicity of area
Thus
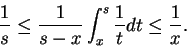 |
(11.8) |
Case 2. If 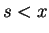 we can reverse the roles of
we can reverse the roles of 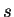 and
and  in equation
(11.8) to get
in equation
(11.8) to get
or
In both cases it follows that
Let 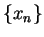 be a generic sequence in
be a generic sequence in
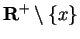 such that
such that
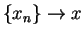 . Then
. Then
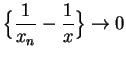 ,
so by
the squeezing rule
,
so by
the squeezing rule
i.e.
Hence
We have proved that
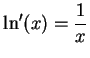 .
. 
11.9
Assumption (Localization rule for derivatives.)
Let
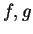
be two real valued functions. Suppose there is some
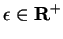
and
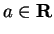
such that
and such that
If

is differentiable at

, then

is differentiable at

and
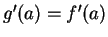
.
This is another assumption that is really a theorem, i.e. it can be
proved. Intuitively this assumption is very plausible.
It says that if two functions agree on an entire interval
centered at  , then their graphs have the same tangents at
, then their graphs have the same tangents at  .
.
11.10
Theorem (Derivative of absolute value.)
Let 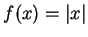 for all
for all
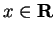 . Then
. Then
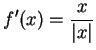 for
all
for
all
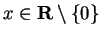 and
and 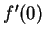 is not defined.
is not defined.
Proof: Since
it follows
from the localization theorem that
To see that  is not differentable at
is not differentable at 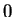 , we want to show that
, we want to show that
does not exist. Let
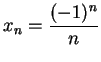 . Then
. Then 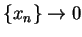 , but
, but
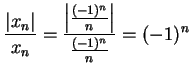 and we know that
and we know that
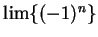 does not exist.
Hence
does not exist.
Hence
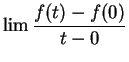 does not exist, i.e.,
does not exist, i.e.,  is not differentiable at
is not differentiable at
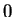 .
.
11.11
Definition (
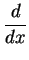 notation for derivatives.)
notation for derivatives.)
An alternate notation for representing derivatives is:
or
This notation is used in the following way
Or:
Let 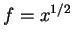 . Then
. Then
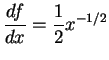 .
.
Let
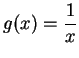 . Then
. Then
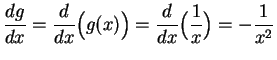 .
.
The
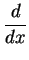 notation is due to
Leibnitz, and is older
than our concept of function.
notation is due to
Leibnitz, and is older
than our concept of function.
Leibnitz wrote the differentiation formulas as ``
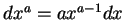 ," or if
," or if
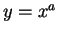 , then ``
, then ``
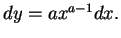 " The notation
" The notation 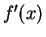 for
derivatives
is due to Joseph Louis
Lagrange (1736-1813).
Lagrange called
for
derivatives
is due to Joseph Louis
Lagrange (1736-1813).
Lagrange called 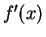 the
derived function of
the
derived function of 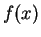 and it is from this that we get our word derivative. Leibnitz called derivatives,
differentials
and Newton
called them fluxions.
and it is from this that we get our word derivative. Leibnitz called derivatives,
differentials
and Newton
called them fluxions.
Many of the early users of the calculus thought of the derivative
as the quotient of two numbers
when 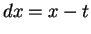 was ``infinitely small''. Today ``infinitely small''
real numbers are out of fashion, but some attempts are being made to
bring them back. Cf Surreal Numbers : How two ex-students turned on to pure
mathematics and found total happiness : a mathematical
novelette, by D. E. Knuth.[30].
or The Hyperreal Line by H. Jerome Keisler[28, pp 207-237].
was ``infinitely small''. Today ``infinitely small''
real numbers are out of fashion, but some attempts are being made to
bring them back. Cf Surreal Numbers : How two ex-students turned on to pure
mathematics and found total happiness : a mathematical
novelette, by D. E. Knuth.[30].
or The Hyperreal Line by H. Jerome Keisler[28, pp 207-237].




Next: 11.2 Some General Differentiation
Up: 11. Calculation of Derivatives
Previous: 11. Calculation of Derivatives
Index
Ray Mayer
2007-09-07
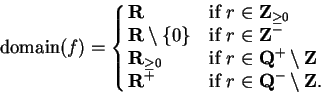
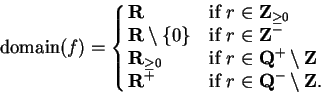
![]() . For all
. For all ![]() in
domain
in
domain
![]() we have
we have
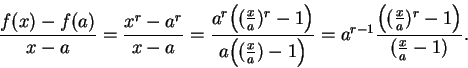
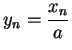 . Then
. Then 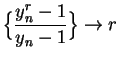 and hence
and hence
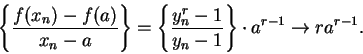
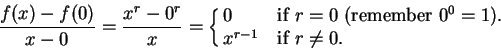
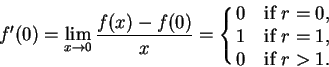
![]() the result is clear, so we assume
the result is clear, so we assume ![]() . For all
. For all
![]() and all
and all
![]() , we have
, we have
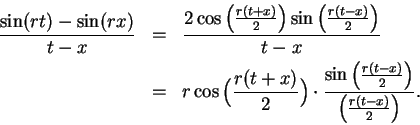
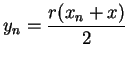 and let
and let
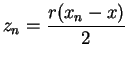 . Then
. Then
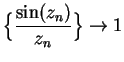 . Hence
. Hence
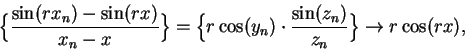
![]() , and let
, and let
![]() . Then
. Then
![]() then
then
![$\displaystyle {A_x^s \Big[ {1\over t}\Big]}$](img2877.gif) represents the area
of the shaded region
represents the area
of the shaded region ![]() in the figure.
in the figure.
![]() we can reverse the roles of
we can reverse the roles of ![]() and
and ![]() in equation
(11.8) to get
in equation
(11.8) to get
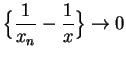 ,
so by
the squeezing rule
,
so by
the squeezing rule
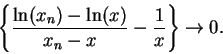
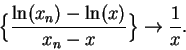
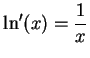 .
. ![]() , then their graphs have the same tangents at
, then their graphs have the same tangents at ![]() .
.
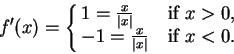
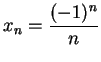 . Then
. Then 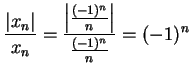 and we know that
and we know that
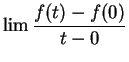 does not exist, i.e.,
does not exist, i.e., 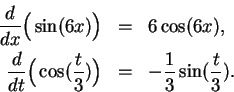
![]() . Then
. Then
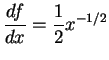 .
.
 . Then
. Then
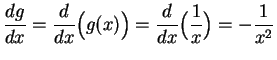 .
.
![]() notation is due to
Leibnitz, and is older
than our concept of function.
notation is due to
Leibnitz, and is older
than our concept of function.
![]() ," or if
," or if
![]() , then ``
, then ``
![]() " The notation
" The notation ![]() for
derivatives
is due to Joseph Louis
Lagrange (1736-1813).
Lagrange called
for
derivatives
is due to Joseph Louis
Lagrange (1736-1813).
Lagrange called ![]() the
derived function of
the
derived function of ![]() and it is from this that we get our word derivative. Leibnitz called derivatives,
differentials
and Newton
called them fluxions.
and it is from this that we get our word derivative. Leibnitz called derivatives,
differentials
and Newton
called them fluxions.