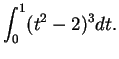Next: 8.3 A Non-integrable Function
Up: 8. Integrable Functions
Previous: 8.1 Definition of the
Index
8.9
Definition (Operations on functions.)
Let
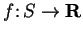
and
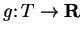
be functions where
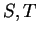
are sets.
Let
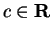
. We define functions
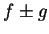
,
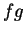
,
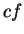
,
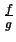
and
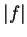
as
follows:
Remark: These operations of addition, subtraction, multiplication
and division for functions satisfy the associative, commutative and
distributive laws that you expect them to. The proofs are straightforward and
will
be omitted.
8.10
Definition (Partition-sample sequence.)
Let
![$[a,b]$](img1071.gif)
be an interval. By a
partition-sample sequence for
![$[a,b]$](img1071.gif)
I
will mean a pair of sequences
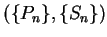
where
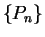
is a sequence
of
partitions of
![$[a,b]$](img1071.gif)
such that
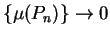
, and for each

in
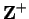
,
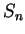
is a sample for
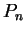
.
8.11
Theorem (Sum theorem for integrable functions.)
Let 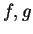 be integrable functions on an interval
be integrable functions on an interval ![$[a,b]$](img1071.gif) . Then
. Then 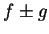 and
and
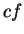 are integrable on
are integrable on ![$[a,b]$](img1071.gif) and
and
and
and
Proof: Suppose  and
and  are integrable on
are integrable on ![$[a,b]$](img1071.gif) . Let
. Let
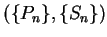 be
a partition-sample sequence for
be
a partition-sample sequence for ![$[a,b]$](img1071.gif) . If
. If
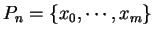 and
and
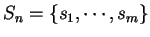 , then
, then
Since  and
and  are integrable, we have
are integrable, we have
By the sum theorem for sequences,
Hence 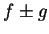 is integrable and
is integrable and
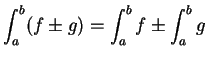 .
The proof of the second statement is left as an exercise.
.
The proof of the second statement is left as an exercise.
8.12
Notation (
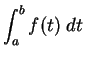 )
)
If

is integrable on an interval
![$[a,b]$](img1071.gif)
we will sometimes write
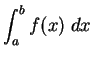
instead of
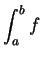
. The ``

" in this expression is
a dummy variable, but the ``
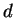
" is a part of the notation and may not be
replaced by another symbol. This notation will be used mainly in cases where
no particular name is available for

. Thus
means
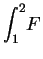
where
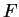
is the function on
![$[1,2]$](img1125.gif)
defined by
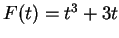
for all
![$t\in [1,2]$](img2042.gif)
. The ``
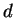
" here stands for difference,
and
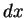
is a ghost of the differences
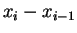
that appear in the
approximations
for the integral. The
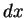
notation is due to Leibniz.
8.13
Example.
Let
This function is integrable over every closed bounded subinterval of
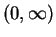
,
since it is a sum of five functions that are known to be
integrable. By several applications of the sum theorem for
integrals we get
8.15
Theorem (Inequality theorem for integrals.) Let  and
and  be integrable functions on the interval
be integrable functions on the interval ![$[a,b]$](img1071.gif) such that
Then
such that
Then
8.16
Exercise.
Prove the inequality theorem for integrals.
A
Proof: We have
Hence by the inequality theorem for integrals
Hence
It follows that
8.18
Theorem.
Let 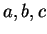 be real numbers with
be real numbers with 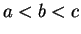 , and let
, and let  be a function
from
be a function
from ![$[a,c]$](img2061.gif) to
to
 . Suppose
. Suppose  is integrable on
is integrable on ![$[a,b]$](img1071.gif) and
and  is
integrable on
is
integrable on
![$[b,c]$](img2062.gif) . Then
. Then  is integrable on
is integrable on ![$[a,c]$](img2061.gif) and
and
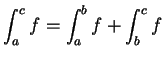 .
.
Proof:
Since  is integrable on
is integrable on ![$[a,b]$](img1071.gif) and on
and on ![$[b,c]$](img2062.gif) , it follows that
, it follows that
 is bounded on
is bounded on ![$[a,b]$](img1071.gif) and on
and on ![$[b,c]$](img2062.gif) , and hence
, and hence  is bounded
on
is bounded
on ![$[a,c]$](img2061.gif) .
Let
.
Let
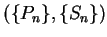 be a partition-sample sequence for
be a partition-sample sequence for ![$[a,c]$](img2061.gif) .
For each
.
For each  in
in
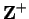 we define a partition
we define a partition 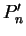 of
of ![$[a,b]$](img1071.gif) and a
partition
and a
partition
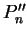 of
of ![$[b,c]$](img2062.gif) , and a sample
, and a sample 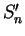 for
for 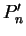 ,
and a
sample
,
and a
sample
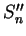 for
for
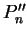 as follows:
as follows:
Then there is an index 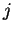 such that
such that
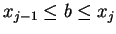 .
.
Let
We have
where
Let 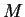 be a bound for
be a bound for  on
on ![$[a,c]$](img2061.gif) . Then
. Then
Also,
Now
Since
it follows from the squeezing rule that
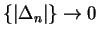 and hence
and hence
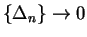 .
.
From equation (8.21)
we have
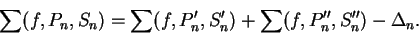 |
(8.22) |
Since
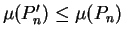 and
and
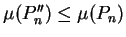 , we
see
that
, we
see
that
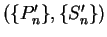 is a partition-sample sequence on
is a partition-sample sequence on
![$[a,b]$](img1071.gif) , and
, and
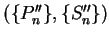 is a partition-sample
sequence on
is a partition-sample
sequence on
![$[b,c]$](img2062.gif) . Since
. Since  was given to be integrable on
was given to be integrable on ![$[a,b]$](img1071.gif) and on
and on ![$[b,c]$](img2062.gif) , we
know
that
, we
know
that
and
Hence it follows from (8.22) that
i.e.,  is integrable on
is integrable on ![$[a,c]$](img2061.gif) and
and
8.24
Definition (Spike function.)
Let
![$[a,b]$](img1071.gif)
be an interval. A function
![$f:[a,b] \to \mbox{{\bf R}}$](img2103.gif)
is called
a
spike function, if there exist numbers
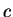
and
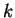
, with
![$c \in [a,b]$](img2104.gif)
such that
Proof: Case 1: Suppose 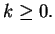 Observe that
Observe that  is increasing on the interval
is increasing on the interval ![$[a,b]$](img1071.gif) and decreasing
on the interval
and decreasing
on the interval ![$[b,c]$](img2062.gif) , so
, so  is integrable on each of these intervals.
The set of points under the graph of
is integrable on each of these intervals.
The set of points under the graph of  is the union of a horizontal
segment and a vertical segment, and thus is a zero-area set. Hence
is the union of a horizontal
segment and a vertical segment, and thus is a zero-area set. Hence
By the previous theorem,  is integrable on
is integrable on ![$[a,c]$](img2061.gif) , and
, and
.
Case 2: Suppose 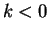 . Then by case 1 we see that
. Then by case 1 we see that 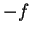 is integrable with
integral equal to zero,
so by the sum theorem for integrals
is integrable with
integral equal to zero,
so by the sum theorem for integrals 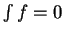 too.
too. 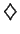
8.28
Exercise.
Prove corollary
8.26, i.e., explain why it follows from theorem
8.25.
8.29
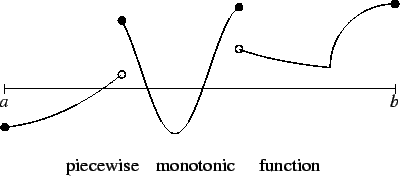
Definition (Piecewise monotonic function.)
A function

from an interval
![$[a,b]$](img1071.gif)
to
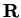
is
piecewise monotonic
if there are points
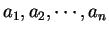
in
![$[a,b]$](img1071.gif)
with
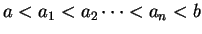
such that

is monotonic on each of the intervals
![$[a,a_1],[a_1,a_2],\cdots
,[a_{n-1},a_n],[a_n,b]$](img2126.gif)
.
8.30
Example.
The function whose graph is sketched below is piecewise monotonic.
8.31
Theorem.
Every piecewise monotonic function is integrable.
Proof: This follows from corollary 8.23. 
8.32
Exercise.
A
Let
Sketch the graph of

. Carefully explain why

is integrable, and find
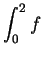
.
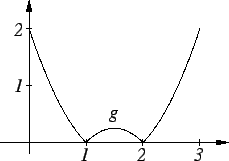
8.33
Example.
Let
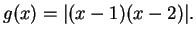
Then
Hence

is integrable on
![$[0,3]$](img2133.gif)
, and




Next: 8.3 A Non-integrable Function
Up: 8. Integrable Functions
Previous: 8.1 Definition of the
Index
Ray Mayer
2007-09-07
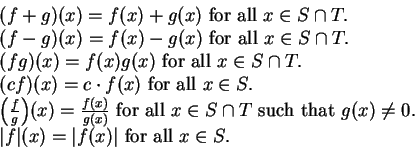
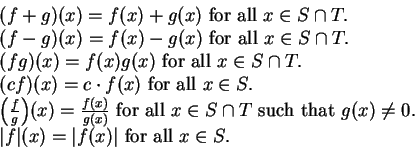
![]() and
and ![]() are integrable on
are integrable on ![]() . Let
. Let
![]() be
a partition-sample sequence for
be
a partition-sample sequence for ![]() . If
. If
![]() and
and
![]() , then
, then
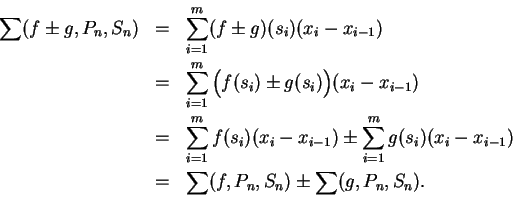
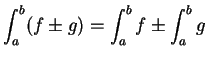 .
The proof of the second statement is left as an exercise.
.
The proof of the second statement is left as an exercise.
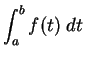 )
If
)
If 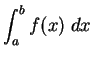 instead of
instead of
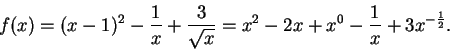
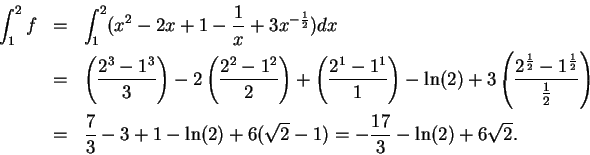
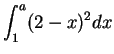 . Here
. Here 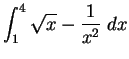 .
.
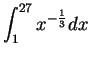 .
.
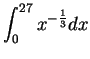 .
.
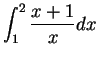 .
.
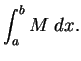 Here
Here 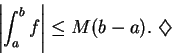
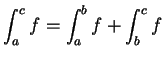 .
.![]() is integrable on
is integrable on ![]() and on
and on ![]() , it follows that
, it follows that
![]() is bounded on
is bounded on ![]() and on
and on ![]() , and hence
, and hence ![]() is bounded
on
is bounded
on ![]() .
Let
.
Let
![]() be a partition-sample sequence for
be a partition-sample sequence for ![]() .
For each
.
For each ![]() in
in
![]() we define a partition
we define a partition ![]() of
of ![]() and a
partition
and a
partition
![]() of
of ![]() , and a sample
, and a sample ![]() for
for ![]() ,
and a
sample
,
and a
sample
![]() for
for
![]() as follows:
as follows:
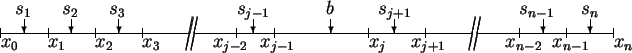
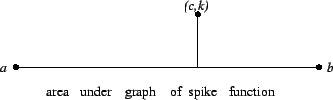
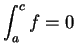 .
.
![]() Observe that
Observe that ![]() is increasing on the interval
is increasing on the interval ![]() and decreasing
on the interval
and decreasing
on the interval ![]() , so
, so ![]() is integrable on each of these intervals.
The set of points under the graph of
is integrable on each of these intervals.
The set of points under the graph of ![]() is the union of a horizontal
segment and a vertical segment, and thus is a zero-area set. Hence
is the union of a horizontal
segment and a vertical segment, and thus is a zero-area set. Hence
![]() . Then by case 1 we see that
. Then by case 1 we see that ![]() is integrable with
integral equal to zero,
so by the sum theorem for integrals
is integrable with
integral equal to zero,
so by the sum theorem for integrals ![]() too.
too. ![]()
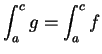 .
.![\begin{displaymath}g(x)=\cases{
f(x) &if $x\in [a,b]\setminus\{a_1,\cdots ,a_n\}...
...
k_j &if $x=a_j$ \mbox{ for some $j$ with $1\leq j\leq n$.}\cr}\end{displaymath}](img2123.gif)
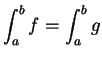 . Thus we
can alter an integrable function on any finite set of points without changing
its integrability or its
integral.
. Thus we
can alter an integrable function on any finite set of points without changing
its integrability or its
integral.
![]()
![\begin{displaymath}g(x) = \cases{
x^2 - 3x + 2 & for $x \in [0,1]$\cr
-x^2 + 3x - 2 & for $x \in [1,2]$\cr
x^2 - 3x + 2 & for $x \in [2,3].$ }
\end{displaymath}](img2131.gif)
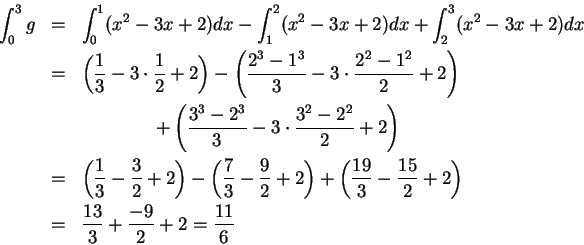
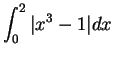 .
.
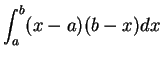 . Here
. Here 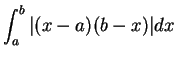 . Here
. Here