If
![]() '', then
'', then ![]() is a true proposition.
is a true proposition.
If
![]() '', then
'', then ![]() is a false proposition.
is a false proposition.
If
![]() '', then
'', then ![]() is a true proposition.
is a true proposition.
If
![]() '', then I will not consider
'', then I will not consider ![]() to
be a proposition (unless lucky
number has been defined.)
to
be a proposition (unless lucky
number has been defined.)
If
![]() '', then
'', then ![]() is a true proposition.
is a true proposition.
If
![]() '', then
'', then ![]() is a false proposition.
is a false proposition.
If
![]() '', then
'', then ![]() is a true proposition.
is a true proposition.
If
![]() '', then I will not consider
'', then I will not consider ![]() to
be a proposition (unless lucky
number has been defined.)
to
be a proposition (unless lucky
number has been defined.)
``![]() and
and ![]() '' is true if and only if both of
'' is true if and only if both of ![]() are true.
are true.
``![]() or
or ![]() '' is true if and only if at least one of
'' is true if and only if at least one of ![]() is true.
is true.
``not ![]() '' is true if and only if
'' is true if and only if ![]() is false.
is false.
Observe that in mathematics, ``or'' is always assumed to be inclusive or:
If ``![]() '' and ``
'' and ``![]() '' are both true, then ``
'' are both true, then ``![]() or
or ![]() '' is true.
'' is true.
``![]() and
and ![]() '' is false.
'' is false.
``![]() or
or ![]() '' is true.
'' is true.
``![]() or
or ![]() '' is true.
'' is true.
``not(not ![]() )'' is true if and only if
)'' is true if and only if ![]() is true.
is true.
For each element ![]() of Q let
of Q let ![]() be the
proposition
be the
proposition
``
![]() ''. Thus
''. Thus
![]() = ``
= ``
![]() '', so
'', so ![]() is true, while
is true, while
![]() = ``
= ``
![]() '', so
'', so ![]() is false.
Here I consider
is false.
Here I consider ![]() to be a rule which assigns to each element
to be a rule which assigns to each element ![]() of Q a proposition
of Q a proposition ![]()
Thus the rule ![]() defined in the previous paragraph is a proposition
form over Q. Note that a proposition form is neither true nor false,
i.e. a proposition form is not a proposition.
defined in the previous paragraph is a proposition
form over Q. Note that a proposition form is neither true nor false,
i.e. a proposition form is not a proposition.
``
![]() '' is true if and only if ((
'' is true if and only if ((![]() are both true)
or (
are both true)
or (![]() are both false)).
are both false)).
Ordinarily one would not make a statement like
``
![]() )''
)''
even though this is a true proposition.
One writes ``
![]() '' in an argument, only
when the person reading the argument can be expected to see the equivalence
of the two statements
'' in an argument, only
when the person reading the argument can be expected to see the equivalence
of the two statements ![]() and
and ![]() .
.
If ![]() and
and ![]() are propositions,then
are propositions,then
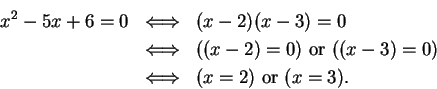
| (3.12) |
| (3.14) |
In proposition 3.16, ![]() is false,
is false, ![]() is true, and
is true, and
![]() is true.
is true.
In proposition 3.17, ![]() is false,
is false, ![]() is false, and
is false, and
![]() is true.
is true.
The usual way to prove
![]() is to
assume that
is to
assume that ![]() is true and show that then
is true and show that then ![]() must be true.
This is sufficient by our convention in (3.11).
must be true.
This is sufficient by our convention in (3.11).
If ![]() and
and ![]() are propositions, then
``
are propositions, then
``
![]() '' is also a proposition, and
'' is also a proposition, and
We will not make much use of the idea of two propositions being equal.
Roughly, two propositions are equal if and only if they are word
for word the same. Thus ``![]() '' and ``
'' and ``![]() '' are not equal
propositions, although they are equivalent. The only time I will
use an ``
'' are not equal
propositions, although they are equivalent. The only time I will
use an ``![]() '' sign between propositions is in definitions. For
example, I might define a proposition form
'' sign between propositions is in definitions. For
example, I might define a proposition form ![]() over N by
saying
over N by
saying
for all
![]()
![]() ``
``![]() '',
'',
or
for all
![]()
![]() .
.
The definition we have given for ``implies'' is a matter of convention,
and there is a school of contemporary mathematicians
(called constructivists)
who define
![]() to be true only if a ``constructive'' argument
can be given that the truth of
to be true only if a ``constructive'' argument
can be given that the truth of ![]() follows from the truth of
follows from the truth of ![]() .
For the constructivists, some of the propositions of the sort we use
are neither true nor false, and some of the theorems we prove are
not provable (or disprovable). A very readable description of the
constructivist point of view can be found in the article Schizophrenia in
Contemporary Mathematics[10, pages 1-10].
.
For the constructivists, some of the propositions of the sort we use
are neither true nor false, and some of the theorems we prove are
not provable (or disprovable). A very readable description of the
constructivist point of view can be found in the article Schizophrenia in
Contemporary Mathematics[10, pages 1-10].
a) Give examples of propositions ![]() such that
``
such that
``
![]() '' and ``
'' and ``
![]() '' are both true, or else
explain why no such examples exist.
'' are both true, or else
explain why no such examples exist.
b) Give examples of propositions ![]() such that ``
such that ``
![]() ''
and ``
''
and ``
![]() '' are both false, or explain why no such
examples exist.
'' are both false, or explain why no such
examples exist.
c) Give examples of propositions ![]() such that ``
such that ``
![]() ''
is true but ``
''
is true but ``
![]() '' is false, or explain why no such
examples exist.
'' is false, or explain why no such
examples exist.
Problem: Let ![]() be the set of all real numbers
be the set of all real numbers ![]() such that
such that
![]() . Describe the set of all elements
. Describe the set of all elements ![]() such that
such that
ARGUMENT A: Let ![]() be an arbitrary element of
be an arbitrary element of ![]() . Then
. Then
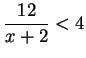 |
|||
ARGUMENT B: Let ![]() be an arbitrary element of
be an arbitrary element of ![]() . Then
. Then
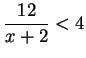 |
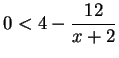 |
||
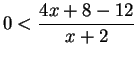 |
|||
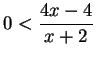 |
|||
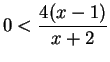 |
|||
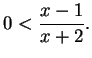 |
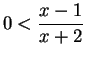 |
|||