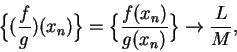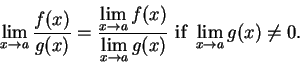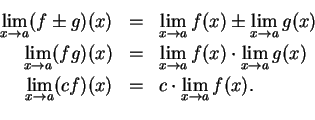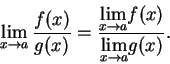Next: 10.3 Definition of the
Up: 10. Definition of the
Previous: 10.1 Velocity and Tangents
Index
Our definition of tangent to a curve is going to be based on the idea of limit. The word limit was used in mathematics long before the
definition we
will give was thought of. One finds statements like `` The limit of a
regular
polygon when the number of sides becomes infinite, is a circle." Early
definitions
of limit often involved the ideas of time or motion. Our definition will be
purely
mathematical.
10.5
Definition (Interior points and approachable points.)
Let
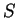
be a subset of
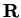
. A
point
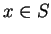
is an
interior point of
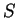
if there is some positive
number
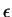
such that the interval
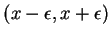
is a subset of
.
A point
is an
approachable point from 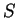
if there is some
positive
number
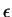
such that either
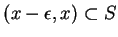
or
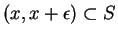
. (Without loss of generality we could replace ``
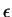
"
in this definition by
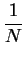
for some
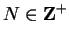
.)
Note that interior points of 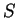 must belong to
must belong to 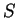 . Approachable points of
. Approachable points of
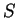 need not belong to
need not belong to 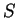 . Any interior point of
. Any interior point of 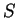 is approachable from
is approachable from
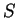 .
.
10.7
Definition (Limit of a function.)
Let

be a real valued function such that
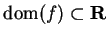
. Let
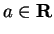
and let
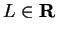
. We say
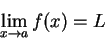 |
(10.8) |
if
- 1)
 is approachable from
is approachable from
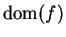 , and
, and
- 2)
- For every sequence
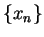 in
in
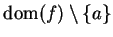
Note that the value of 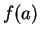 (if it exists) has no influence on the meaning of
(if it exists) has no influence on the meaning of
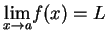 . Also the ``
. Also the ``  " in (10.8) is a dummy
variable, and can be replaced by any other symbol that has no assigned meaning.
" in (10.8) is a dummy
variable, and can be replaced by any other symbol that has no assigned meaning.
10.9
Example.
For all
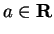
we have
Also
and
by lemma
9.34. Also
by theorem
9.37.
10.10
Example.
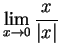
is not defined.
Let
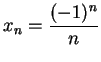
. Then
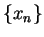
is a sequence in
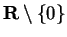
, and
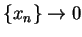
and
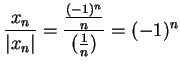
. We know there is no number
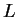
such that
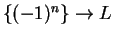
.
10.11
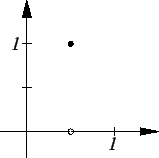
Example.
Let

be the spike function
Then
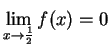
,
since if
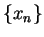
is a generic sequence in
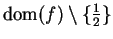
, then
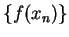
is the constant sequence
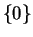
.
10.12
Example.
The limit
does not exist. If
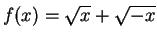
, then the domain of

consists of the single point
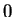
, and
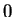
is not approachable from
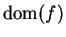
.
If we did not have condition
1) in our definition, we would have
which would not be a good thing. (If there are no sequences in
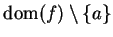
, then
is true, no matter what
statement about
![$\{x_n\}{]}$](img2699.gif)
is.)
In this course we will not care much about functions like
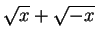 .
.
10.13
Example.
I will show that
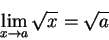 |
(10.14) |
for all
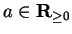
.
Case 1: Suppose
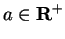 . Let
. Let 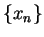 be a generic sequence in
be a generic sequence in
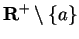 such that
such that 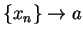 . Then
. Then
Now, since
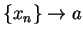
, we have
so by the squeezing rule
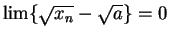
which is equivalent to
This proves (
10.14) when
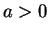
.
Case 2: Suppose 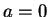 .
The domain of the square root function is
.
The domain of the square root function is 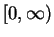 , and
, and 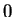 is approachable
from this set.
is approachable
from this set.
Let 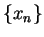 be a sequence in
be a sequence in
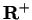 such that
such that 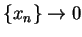 . To show that
. To show that
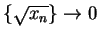 , I'll use the definition of limit. Let
, I'll use the definition of limit. Let
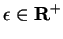 . Then
. Then
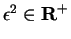 , so by the definition of
convergence,
there is an
, so by the definition of
convergence,
there is an
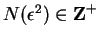 such that for all
such that for all
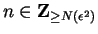 we have
we have
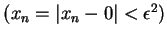 .
Then
for all
.
Then
for all
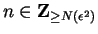 we have
we have
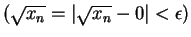 and hence
and hence
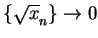 .
. 
Many of our rules for limits of sequences have immediate corollaries as
rules
for limits of functions. For example, suppose 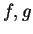 are real valued functions with
are real valued functions with
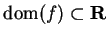 and
and
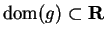 . Suppose
. Suppose
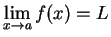 and
and
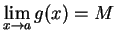 . Let
. Let 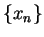 be a generic sequence in
be a generic sequence in
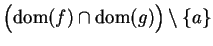 such that
such that 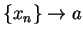 . Then
. Then 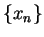 is a
sequence in
is a
sequence in
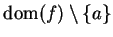 and
and 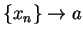 , so
, so
Also 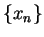 is a sequence in
is a sequence in
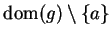 and
and 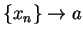 so
so
By the sum and product rules for sequences, for any
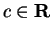
and
and thus we've proved that
and
Moreover if
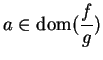 (so that
(so that 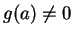 ), and if
), and if
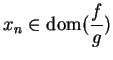 for all
for all 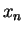 (so that
(so that 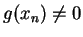 for all
for all
 ),
it follows from the quotient rule for sequences that
),
it follows from the quotient rule for sequences that
so that
Actually all of the results just claimed are not quite true as stated. For we
have
and
but
The correct theorem
is:
Proof: Most of the theorem follows from the remarks made above. We will assume
the remaining parts.
10.16
Theorem (Inequality rule for limits of functions.) Let  and
and  be
real functions with
be
real functions with
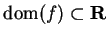 and
and
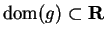 .
Suppose that
.
Suppose that
- i
-
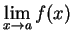 and
and
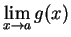 both
exist.
both
exist.
- ii
 is approachable from
is approachable from
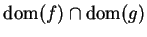 .
.
- iii
- There is a positive number
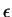 such that
such that
Then
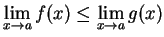 .
.
Proof: Let 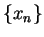 be a sequence in
be a sequence in
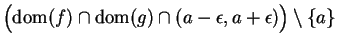 such that
such that 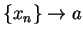 .
Then
.
Then 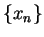 is a sequence in
is a sequence in
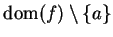 that converges
to
that converges
to  , so by the definition of limit of a function,
, so by the definition of limit of a function,
Similiarly
Also
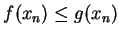 for all
for all  , so it follows from the inequality
rule for limits of sequences that
, so it follows from the inequality
rule for limits of sequences that
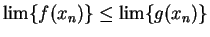 ,
i.e.
,
i.e.
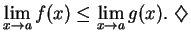 .
.
10.17
Theorem (Squeezing rule for limits of functions.) Let  ,
,  and
and 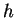 be
real functions with
be
real functions with
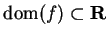 ,
,
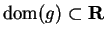 ,
and
,
and
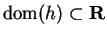 .
Suppose that
.
Suppose that
- i
-
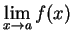 and
and
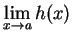 both
exist and are equal.
both
exist and are equal.
- ii
 is approachable from
is approachable from
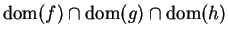 .
.
- iii
- There is a positive number
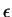 such that
such that
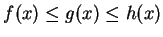 for all
for all  in
in
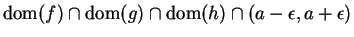 .
.
Then
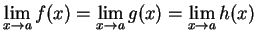 .
.
Proof: The proof is almost identical to the proof of theorem 10.16.




Next: 10.3 Definition of the
Up: 10. Definition of the
Previous: 10.1 Velocity and Tangents
Index
Ray Mayer
2007-09-07
![]() must belong to
must belong to ![]() . Approachable points of
. Approachable points of
![]() need not belong to
need not belong to ![]() . Any interior point of
. Any interior point of ![]() is approachable from
is approachable from
![]() .
.
![]() is the closed interval
is the closed interval ![]() then the points that are approachable
from
then the points that are approachable
from ![]() are exactly the points in
are exactly the points in ![]() , and the interior points of
, and the interior points of ![]() are the
points in
the open interval
are the
points in
the open interval ![]() .
.
![]() (if it exists) has no influence on the meaning of
(if it exists) has no influence on the meaning of
![]() . Also the ``
. Also the `` ![]() " in (10.8) is a dummy
variable, and can be replaced by any other symbol that has no assigned meaning.
" in (10.8) is a dummy
variable, and can be replaced by any other symbol that has no assigned meaning.
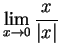 is not defined. Let
is not defined. Let
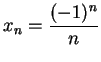 . Then
. Then 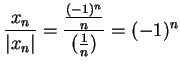 . We know there is no number
. We know there is no number 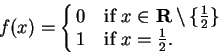
![]() .
.
![]() . Let
. Let ![]() be a generic sequence in
be a generic sequence in
![]() such that
such that ![]() . Then
. Then
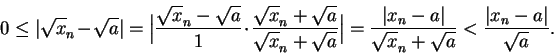
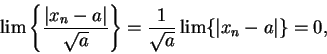
![]() .
The domain of the square root function is
.
The domain of the square root function is ![]() , and
, and ![]() is approachable
from this set.
is approachable
from this set.
![]() be a sequence in
be a sequence in
![]() such that
such that ![]() . To show that
. To show that
![]() , I'll use the definition of limit. Let
, I'll use the definition of limit. Let
![]() . Then
. Then
![]() , so by the definition of
convergence,
there is an
, so by the definition of
convergence,
there is an
![]() such that for all
such that for all
![]() we have
we have
![]() .
Then
for all
.
Then
for all
![]() we have
we have
![]() and hence
and hence
![]() .
. ![]()
![]() are real valued functions with
are real valued functions with
![]() and
and
![]() . Suppose
. Suppose
![]() and
and
![]() . Let
. Let ![]() be a generic sequence in
be a generic sequence in
![]() such that
such that ![]() . Then
. Then ![]() is a
sequence in
is a
sequence in
![]() and
and ![]() , so
, so
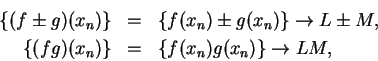
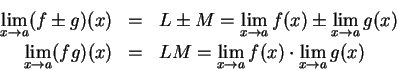
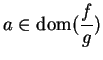 (so that
(so that 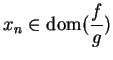 for all
for all