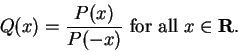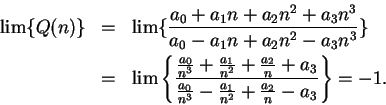14.7
Example.
Two points
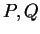
on a sphere are called
antipodal points if
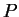
and
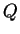
are opposite ends of the same diameter
of the sphere. We will consider the surface of the earth to be a sphere
of radius
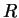
. At any fixed time, let
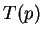
denote the temperature
of the earth at the point
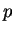
on the surface of the earth. (More precisely,
let
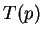
be the number such that the temperature at
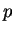
is
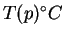
).
We will show that there are two antipodal points
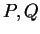
on the surface of
the earth such that
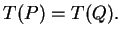
In fact, we will show that there are two
antipodal points on the equator with the same temperature. We first introduce
a coordinate system so that the center of the earth is at the origin,
and the plane of the equator is the

-
plane, and the point on the
equator passing through the Greenwich meridian is the point
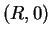
.
Then the points on the equator are the points
Define a function
![$f: [0,\pi] \to \mbox{{\bf R}}$](img3466.gif)
by
Thus
We suppose that

is a continuous function on
![$[0,\pi]$](img2542.gif)
.
If
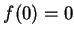
then
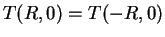
, so
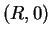
and
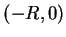
are a pair
of antipodal points with the same temperature. Now
so if
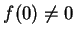
then
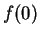
and
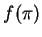
have opposite signs. Hence by the
intermediate value property, there is a number
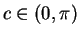
such that
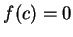
, i.e.
Then
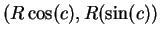
and
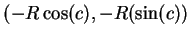
are a pair of
antipodal points with the same temperature.
14.8
Example.
Let
where
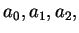
and
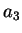
are real numbers, and
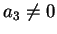
.
Then there exists some number
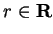
such that
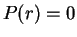
.
Proof: I will suppose that 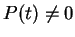 for all
for all
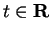 and
derive a contradiction. Let
and
derive a contradiction. Let
Since
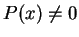
for all
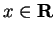
,
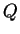
is continuous on
R. We know that
Hence
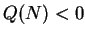
for some
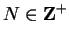
. Then
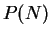
and
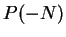
have
opposite signs, so by the intermediate value property there
is a number
![$r \in [-N,N]$](img3492.gif)
such that
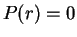
. This contradicts
our assumption that
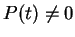
for all
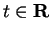
.
14.10
Exercise.
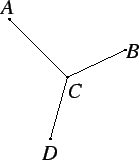
A
Three wires
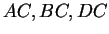
are joined at a common
point
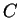
.
Let
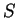
be the Y-shaped figure formed by the three wires.
Prove that at any time there are two points in
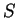
with the same temperature.
14.11
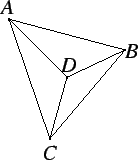
Exercise.
A
Six wires are joined to form the figure
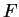
shown in the diagram.
Show that at any time there are three points in
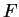
that have the same temperature. To simplify the problem, you may assume
that the temperatures at
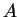
,
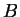
,
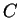
, and
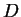
are all distinct.
![]() for all
for all
![]() and
derive a contradiction. Let
and
derive a contradiction. Let