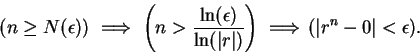Next: 6.6 Geometric Series
Up: 6. Limits of Sequences
Previous: 6.4 Properties of Limits.
Index
6.50
Example.
In example
6.20, we used the definition of limit to show that
for all
, and claimed that a similar argument shows that
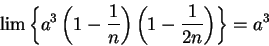 |
(6.51) |
We will now use the basic properties of limits to prove (
6.51).
By the product rule and the null
sequence rule,
Hence by the sum rule
By the sum rule and the null sequence rule
Hence by the product rule,
Now
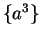
is a constant sequence,
so by the product rule,
6.52
Example.
In the previous example, I made at least eight applications of our limit
rules.
However, the applications are completely mechanical so I will usually not be so
careful, and in a situation like this, I will just write
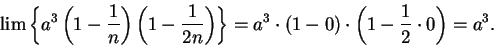 |
(6.53) |
The argument given in equation (6.53) looks remarkably similar
to the eighteenth century argument given in example 6.25.
6.54
Example.
Let

be a positive number,
and let
In (
2.13), we showed that
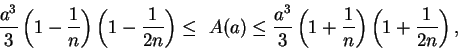 |
(6.55) |
for all
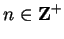
, and claimed that these
inequalities show that
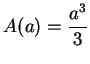
.
Now I want to examine the claim more closely.
In example 6.20 we proved that
and in example
6.50 we proved that
By applying the squeezing rule to equation
6.55, we see that
i.e.
6.56
Example.
I will now consider the limit
Here I cannot apply the quotient rule for sequences, because the limits of the
numerator and denominator do not exist. However, I notice that I can simplify
my
sequence:
I will now use a trick.
I will factor the highest power of

out of the
numerator and denominator:
It is now clear what the limit is.
6.57
Example.
I want to investigate
I'll apply the factoring trick of the previous example.
so
6.58
Example.
I want to find
I observe that
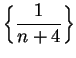
is a translate of
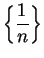
so by the translation rule
I can also try to do this by my factoring trick:
6.60
Example.
Let

be a real number greater than
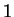
, and let
In (
2.34) we showed that
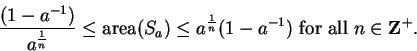 |
(6.61) |
I want to conclude from this that
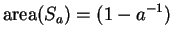
.
By the  th root rule, and the quotient and product rules, we have
th root rule, and the quotient and product rules, we have
and
By (
6.61) and the squeezing rule, we conclude that
i.e.
6.62
Example.
Let the sequence
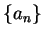
be defined by the rules
Thus, for example
and
It is clear that
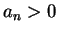
for all

in
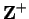
. Let
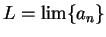
. Then by
the
translation rule,
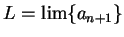
also.
From (
6.63) we have
Thus
i.e.
Hence
Thus
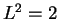
, and it follows that
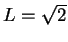
or
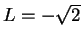
.
But we noticed above that
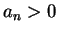
for all

in
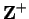
, and hence by the
inequality
rule for sequences,
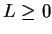
. Hence we conclude that
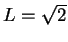
, i.e.,
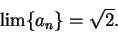 |
(6.64) |
(Actually there is an error in the reasoning here, which you should try to
find, but
the
conclusion (
6.64) is in fact correct. After you have
done exercise
6.68, the error should become apparent.)
6.65
Exercise.
Use a calculator to find
the first six terms of the
sequence
(
6.63). Do all calculations using all the accuracy your calculator
allows, and write down the results to all the accuracy you can get. Compare
your
answers with
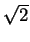
(as given by your calculator) and for each term note how
many decimal places accuracy you have.
6.66
Example.
Let
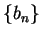
be the sequence defined by the rules
Thus, for example
and
Notice that
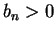
for all

. Let
By the translation rule
By (
6.67) (with

replaced by
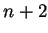
), we have
Hence
Thus
By the quadratic formula
Since
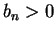
for all

, we have
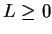
, so we have
(This example has the same error as the previous one.)
6.68
Exercise.
Repeat exercise
6.65
using the sequence
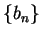
described in (
6.67) in place of the sequence
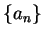
, and
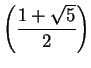
in place of
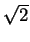
.
After doing this problem, you should be able to point out the
error in examples (
6.62) and (
6.66).
(This example is rather
surprising. I took it from [
14, page 55, exercise 20].)
6.70
Exercise.
Let

and
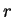
be positive numbers and let
In (
2.4) we showed that
Use this result, together with the power sums listed in
Bernoulli' table
to find the area of
![$S_0^a[t^3]$](img1722.gif)
.
6.71
Theorem ( th power theorem.)
Let
th power theorem.)
Let 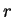 be a real number such that
be a real number such that 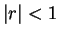 . Then
. Then
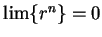 .
.
Proof: Let
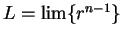 . Now
. Now 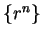 is a translate of
is a translate of
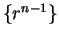 , so
by the translation theorem
, so
by the translation theorem
so we have 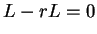 or
or
We assumed that 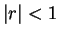 , so
, so 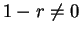 , and hence it follows that
, and hence it follows that 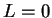 .
. 
The proof just given is not valid. In fact, the argument shows that
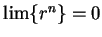 whenever
whenever 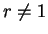 , and this is certainly wrong when
, and this is certainly wrong when 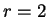 .
The
error comes in the first sentence, `` Let
.
The
error comes in the first sentence, `` Let
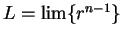 ''. The
argument
works if the sequence
''. The
argument
works if the sequence 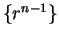 or
or 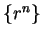 converges. We will now give a
second (correct) proof of theorem 6.71.
converges. We will now give a
second (correct) proof of theorem 6.71.
Second Proof: Let 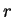 be a real number with
be a real number with 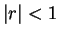 .
If
.
If 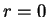 , then
, then
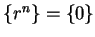 is a constant sequence, and
is a constant sequence, and
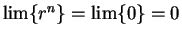 . Hence the theorem holds when
. Hence the theorem holds when 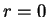 ,
and we may assume that
,
and we may assume that 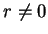 .
Let
.
Let 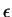 be a generic positive number,
If
be a generic positive number,
If
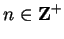 we have
we have
Now since 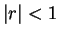 , we know that
, we know that 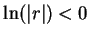 and hence
and hence
By the Archimedean property, there is some positive integer 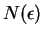 such
that
such
that
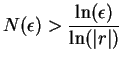 .
Then for all
.
Then for all  in
in
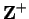
Hence 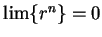 .
. 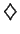
6.72
Exercise.
Why was it necessary to make
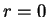
a special case in the Second Proof
above?




Next: 6.6 Geometric Series
Up: 6. Limits of Sequences
Previous: 6.4 Properties of Limits.
Index
Ray Mayer
2007-09-07
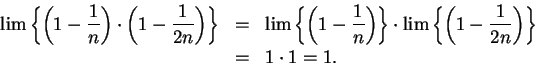
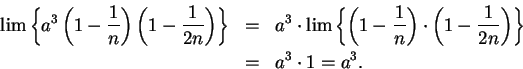
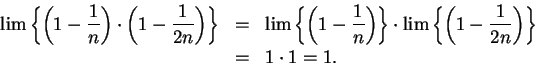
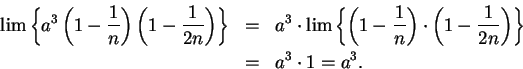
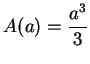 .
Now I want to examine the claim more closely.
.
Now I want to examine the claim more closely.
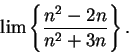
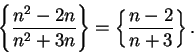
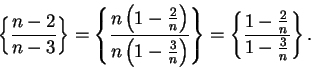
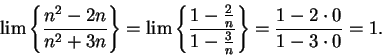
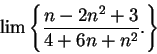
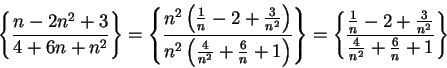
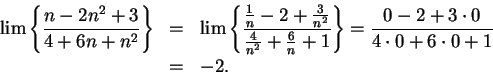
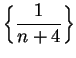 is a translate of
is a translate of
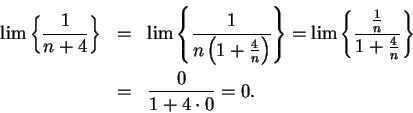
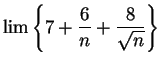
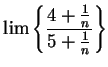
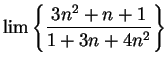
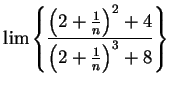
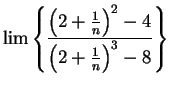
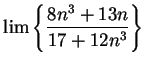
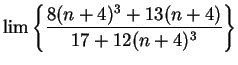
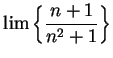 .
.
![]() th root rule, and the quotient and product rules, we have
th root rule, and the quotient and product rules, we have
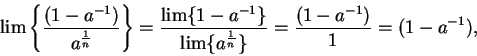
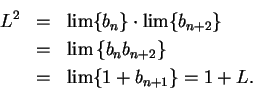
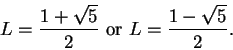
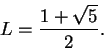
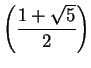 in place of
in place of ![]() . Now
. Now ![]() is a translate of
is a translate of
![]() , so
by the translation theorem
, so
by the translation theorem
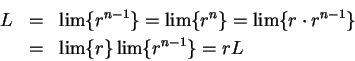
![]() whenever
whenever ![]() , and this is certainly wrong when
, and this is certainly wrong when ![]() .
The
error comes in the first sentence, `` Let
.
The
error comes in the first sentence, `` Let
![]() ''. The
argument
works if the sequence
''. The
argument
works if the sequence ![]() or
or ![]() converges. We will now give a
second (correct) proof of theorem 6.71.
converges. We will now give a
second (correct) proof of theorem 6.71.
![]() be a real number with
be a real number with ![]() .
If
.
If ![]() , then
, then
![]() is a constant sequence, and
is a constant sequence, and
![]() . Hence the theorem holds when
. Hence the theorem holds when ![]() ,
and we may assume that
,
and we may assume that ![]() .
Let
.
Let ![]() be a generic positive number,
If
be a generic positive number,
If
![]() we have
we have
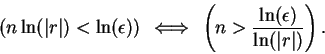
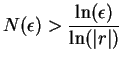 .
Then for all
.
Then for all