Next: 6.5 Illustrations of the
Up: 6. Limits of Sequences
Previous: 6.3 Convergence of Sequences
Index
In this section I will state some basic
properties of limits. All of the statements listed here as assumptions
are, in fact, theorems that can be proved from the definition of limits.
I am omitting the proofs because of lack of time, and because the results
are so plausible that you will probably believe them without a proof.
6.35
Definition (Constant sequence.)
If
is a real number then the sequence
all of whose terms are equal to
is called a
constant
sequence
It is an immediate consequence of the definition of convergence that
for every real number 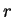 . (If
. (If 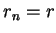 for all
for all  in
in
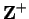 then
then
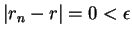 for all
for all 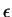 in
in
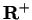 so
so 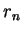 approximates
approximates
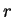 with an error smaller than
with an error smaller than 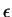 for all
for all 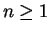 .
. 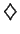 .)
.)
We have just proved
6.36
Theorem (Constant sequence rule.) If 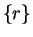 denotes a constant sequence of real numbers, then
denotes a constant sequence of real numbers, then
6.37
Theorem (Null sequence rule.) Let 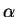 be a positive rational number. Then
be a positive rational number. Then
Proof: Let 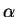 be a positive rational number, and let
be a positive rational number, and let 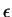 be a
generic positive number. By the
monotonicity of powers
, we hwve
be a
generic positive number. By the
monotonicity of powers
, we hwve
By the Archimedian property for
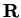 there is an integer
there is an integer 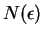 in
in
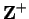 such that
such that
Then for all  in
in
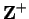
Thus
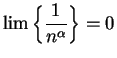 .
. 
6.38
Assumption (Sum rule for sequences.)
Let
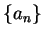
and
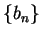
be convergent sequences of real numbers. Then
and
The sum rule is actually easy to prove, but I will not prove it.
(You can probably supply a proof
for it.)
Notice the hypothesis that 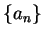 and
and 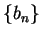 are convergent
sequences. It is not true in general that
are convergent
sequences. It is not true in general that
For example, the statement
is false, since
but neither of the limits
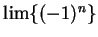 or
or
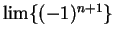 exist.
exist.
6.39
Assumption (Product rule for sequences.)
Let
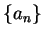
and
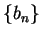
be convergent sequences. Then
An important special case of the product rule occurs when one of the
sequences is constant:
If  is a real number, and
is a real number, and 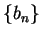 is a convergent sequence, then
is a convergent sequence, then
The intuitive content of the product rule is that if 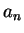 approximates
approximates
 very well, and
very well, and 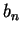 approximates
approximates 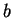 very well, then
very well, then 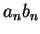 approximates
approximates 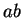 very well. It is somewhat tricky to prove this for a
reason that is illustrated by the following example.
very well. It is somewhat tricky to prove this for a
reason that is illustrated by the following example.
According to Maple,
so 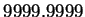 approximates
approximates
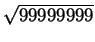 with 4 decimal accuracy.
Let
with 4 decimal accuracy.
Let
and let
Then  approximates
approximates 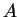 with 4 decimal accuracy and
with 4 decimal accuracy and 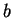 approximates
approximates
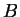 with 4 decimal accuracy. But
with 4 decimal accuracy. But
and
so 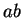 does not approximate
does not approximate 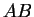 with an accuracy of even one
decimal.
with an accuracy of even one
decimal.
6.40
Assumption (Quotient rule for sequences.)
Let
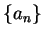
and
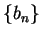
be convergent real sequences such that
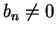
for all

in
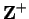
and
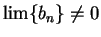
. Then
The hypotheses here are to be expected. If some term 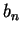 were zero,
then
were zero,
then
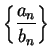 would not be a sequence,
and if
would not be a sequence,
and if 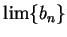 were zero, then
were zero, then
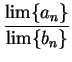 would not be defined.
would not be defined.
6.41
Assumption (Inequality rule for sequences.)
Let
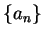
and
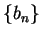
be convergent sequences. Suppose there is an
integer
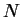
in
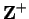
such that
Then
The most common use of this rule is in situations where
and we conclude that
6.42
Assumption (Squeezing rule for sequences.)
Let
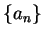
,
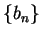
, and
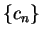
be three real sequences.
Suppose there is an integer
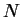
in
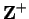
such that
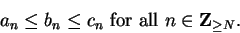 |
(6.43) |
Suppose further, that
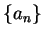
and
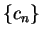
both
converge to the same limit
.
Then
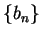
also converges to
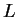
.
If we knew that the middle sequence, 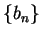 in the squeezing rule was
convergent, then we would be able to prove the squeezing rule from the
inequality rule, since if all three sequences
in the squeezing rule was
convergent, then we would be able to prove the squeezing rule from the
inequality rule, since if all three sequences
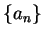 ,
, 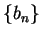 and
and 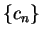 converge, then it follows from
(6.43) that
converge, then it follows from
(6.43) that
i.e.
and hence
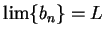 . The power of the squeezing rule is that
it allows us to conclude that a limit exists.
. The power of the squeezing rule is that
it allows us to conclude that a limit exists.
6.44
Definition (Translate of a sequence.)
Let
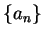
be a real sequence, and let
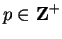
. The sequence
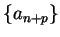
is called a
translate of
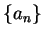
.
6.45
Example.
If
then
If
then
6.46
Theorem (Translation rule for sequences.) Let 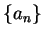 be a convergent sequence of real numbers, and let
be a convergent sequence of real numbers, and let 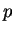 be a
positive integer. Then
be a
positive integer. Then 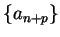 is convergent and
is convergent and
Proof: Suppose 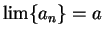 , and let
, and let 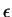 be a generic element
in
be a generic element
in
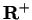 . Then we can find an integer
. Then we can find an integer 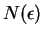 in
in
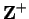 such that
such that
If
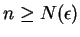 then
then
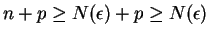 so
so
This shows that
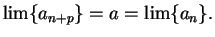
6.47
Example.
The sequence
is a translate of the sequence
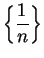
. Since
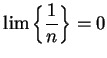
it follows from the translation
theorem that
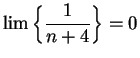
also.
6.48
Theorem ( th root rule for sequences.) Let
th root rule for sequences.) Let  be a positive number then
be a positive number then
Proof: Case 1: Suppose 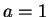 . Then
. Then
Case 2: Suppose 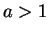 , so that
, so that
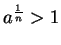 for all
for all
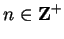 .
Let
.
Let 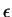 be a generic positive number, and let
be a generic positive number, and let  be a generic
element of
be a generic
element of
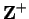 .
Since
.
Since 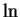 is strictly
increasing on
is strictly
increasing on
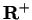 we have
we have
(In the last step I used the fact that
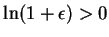 if
if 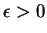 .)
By the Archimedean property for
.)
By the Archimedean property for
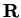 there is an integer
there is an integer 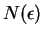 in
in
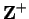 such that
such that
For all
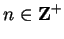 we have
we have
Hence
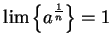 .
.
Case 3: Suppose 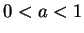 . Then
. Then 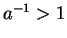 so by Case 2, we have
so by Case 2, we have
Thus, in all cases, we have




Next: 6.5 Illustrations of the
Up: 6. Limits of Sequences
Previous: 6.3 Convergence of Sequences
Index
Ray Mayer
2007-09-07
![]() be a positive rational number, and let
be a positive rational number, and let ![]() be a
generic positive number. By the
monotonicity of powers
, we hwve
be a
generic positive number. By the
monotonicity of powers
, we hwve
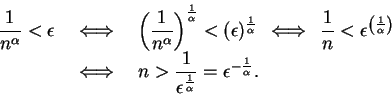
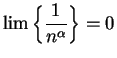 .
. ![]() and
and ![]() are convergent
sequences. It is not true in general that
are convergent
sequences. It is not true in general that
![]() is a real number, and
is a real number, and ![]() is a convergent sequence, then
is a convergent sequence, then
![]() approximates
approximates
![]() very well, and
very well, and ![]() approximates
approximates ![]() very well, then
very well, then ![]() approximates
approximates ![]() very well. It is somewhat tricky to prove this for a
reason that is illustrated by the following example.
very well. It is somewhat tricky to prove this for a
reason that is illustrated by the following example.
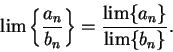
![]() were zero,
then
were zero,
then
 would not be a sequence,
and if
would not be a sequence,
and if ![]() were zero, then
were zero, then
 would not be defined.
would not be defined.
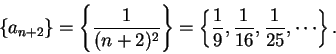
![]() , and let
, and let ![]() be a generic element
in
be a generic element
in
![]() . Then we can find an integer
. Then we can find an integer ![]() in
in
![]() such that
such that
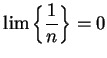 it follows from the translation
theorem that
it follows from the translation
theorem that
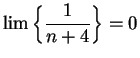 also.
also.
![]() . Then
. Then
![]() , so that
, so that
![]() for all
for all
![]() .
Let
.
Let ![]() be a generic positive number, and let
be a generic positive number, and let ![]() be a generic
element of
be a generic
element of
![]() .
Since
.
Since ![]() is strictly
increasing on
is strictly
increasing on
![]() we have
we have
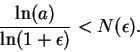
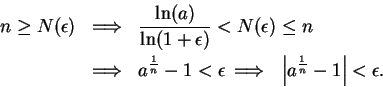
![]() . Then
. Then ![]() so by Case 2, we have
so by Case 2, we have