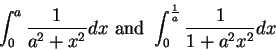Next: 8.6 Integrals and Area
Up: 8. Integrable Functions
Previous: 8.4 The Ruler Function
Index
8.42
Definition (Stretch of a function.)
Let
![$[a,b]$](img1071.gif)
be an interval in
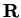
, let
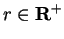
, and let
![$f\colon
[a,b]\to\mbox{{\bf R}}$](img2208.gif)
. We define a new function
![$f_r\colon [ra,rb]\to\mbox{{\bf R}}$](img2209.gif)
by
If
![$t\in [ra,rb]$](img2211.gif)
, then
![$\displaystyle {{t\over r}\in [a,b]}$](img2212.gif)
,
so
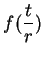
is defined.
The graph of 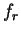 is obtained by stretching the graph of
is obtained by stretching the graph of  by a factor of
by a factor of
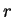 in
the horizontal direction, and leaving it unstretched in the vertical direction.
(If
in
the horizontal direction, and leaving it unstretched in the vertical direction.
(If 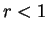 the stretch is actually a shrink.) I will call
the stretch is actually a shrink.) I will call 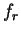 the stretch of
the stretch of
 by
by 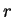 .
.
Proof: Suppose  is integrable on
is integrable on ![$[a,b]$](img1071.gif) . Let
. Let
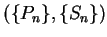 be an
arbitrary partition-sample sequence for
be an
arbitrary partition-sample sequence for ![$[ra,rb]$](img2217.gif) . If
. If
let
Then
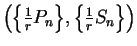 is a
partition-sample sequence for
is a
partition-sample sequence for ![$[a,b]$](img1071.gif) , so
, so
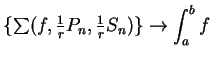 .
Now
.
Now
so
This shows that 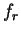 is integrable on
is integrable on ![$[ra,rb]$](img2217.gif) , and
, and
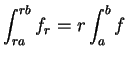 .
. 
Remark: The notation 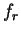 is not a standard notation for
the stretch of a function, and I will not use this notation in the future.
I will usually use the change of scale theorem in the form of equation
(8.44), or in the equivalent form
is not a standard notation for
the stretch of a function, and I will not use this notation in the future.
I will usually use the change of scale theorem in the form of equation
(8.44), or in the equivalent form
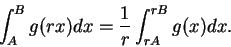 |
(8.45) |
8.46
Exercise.
A
Explain why formula (
8.45)
is equivalent to
formula (
8.44).
8.47
Example.
We define
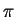
to be the area of the unit
circle. Since the unit circle is
carried to itself by reflections about the horizontal and vertical axes, we
have
Since points in the unit circle satisfy
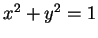
or
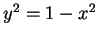
, we get
We will use this result to calculate the area of a circle of radius

. The
points on the circle with radius

and center
0 satisfy
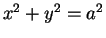
, and by the same
symmetry
arguments we just gave
By the change of scale theorem
The formulas
or more generally
are worth remembering. Actually, these are cases of a formula you already know,
since
they say that the area of a circle of radius

is
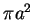
.
8.48
Exercise.
A
Let
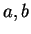
be positive numbers and let
be the set of points
inside the
ellipse whose equation is
Calculate the area of
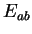
.
8.49
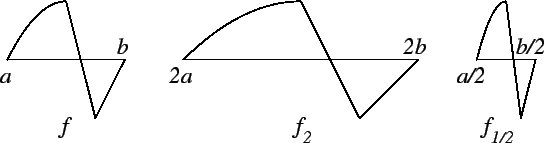
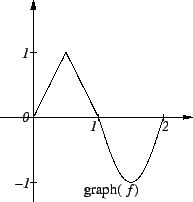
Exercise.
The figure shows the graph of a function

.
Let functions

,
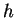
,
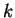
,
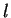
, and
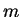
be defined by
- a)
-
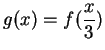 .
.
- b)
-
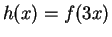 .
.
- c)
-
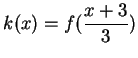 .
.
- d)
-
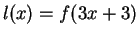 .
.
- e)
-
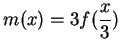 .
.
Sketch the graphs of

,
,
,
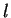
, and
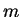
on different axes.
Use the same scale for all of the graphs, and use the same scale
on the

-axis and the
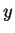
-axis,
8.50
Exercise.
A
The value of
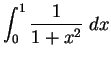
is
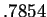
(approximately). Use this fact to calculate approximate
values for
where
. Find numerical values for both of
these integrals when
.




Next: 8.6 Integrals and Area
Up: 8. Integrable Functions
Previous: 8.4 The Ruler Function
Index
Ray Mayer
2007-09-07
![$\displaystyle {{t\over r}\in [a,b]}$](img2212.gif) ,
so
,
so
![]() is obtained by stretching the graph of
is obtained by stretching the graph of ![]() by a factor of
by a factor of
![]() in
the horizontal direction, and leaving it unstretched in the vertical direction.
(If
in
the horizontal direction, and leaving it unstretched in the vertical direction.
(If ![]() the stretch is actually a shrink.) I will call
the stretch is actually a shrink.) I will call ![]() the stretch of
the stretch of
![]() by
by ![]() .
.
![$\displaystyle {{t\over r}\in [a,b]}$](img2212.gif) ,
so
,
so

![]() is obtained by stretching the graph of
is obtained by stretching the graph of ![]() by a factor of
by a factor of
![]() in
the horizontal direction, and leaving it unstretched in the vertical direction.
(If
in
the horizontal direction, and leaving it unstretched in the vertical direction.
(If ![]() the stretch is actually a shrink.) I will call
the stretch is actually a shrink.) I will call ![]() the stretch of
the stretch of
![]() by
by ![]() .
.
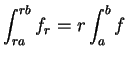 ,
i.e.,
,
i.e.,
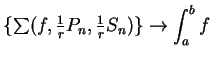 .
Now
.
Now
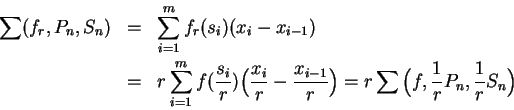
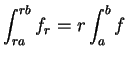 .
. ![]() is not a standard notation for
the stretch of a function, and I will not use this notation in the future.
I will usually use the change of scale theorem in the form of equation
(8.44), or in the equivalent form
is not a standard notation for
the stretch of a function, and I will not use this notation in the future.
I will usually use the change of scale theorem in the form of equation
(8.44), or in the equivalent form
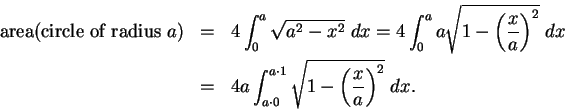
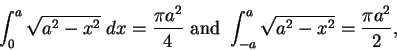
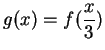 .
.
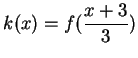 .
.
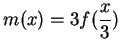 .
.
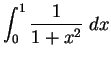 is
is