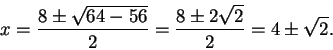Even though you are probably familiar with the Pythagorean theorem, the result is so important and non-obvious that I am including a proof of it.
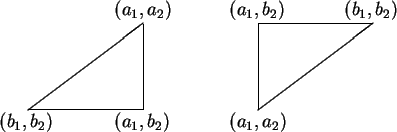
Proof: Consider a right triangle ![]() whose legs have length
whose legs have length ![]() and
and
![]() , and whose hypotenuse has length
, and whose hypotenuse has length ![]() , and whose angles are
, and whose angles are ![]() and
and
![]() as shown in the figure.
as shown in the figure.
We have
![]() since
since ![]() is a right triangle.
is a right triangle.
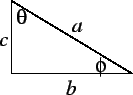
The proof just given uses a combination of algebra and geometry. I will now give a second proof that is completely geometrical.
Construct a second square ![]() with sides of length
with sides of length ![]() , and mark off
segments
, and mark off
segments ![]() and
and ![]() of length
of length ![]() as shown in figure 2.
Then draw
as shown in figure 2.
Then draw ![]() perpendicular to
perpendicular to ![]() and let
and let ![]() intersect
intersect ![]() at
at ![]() , and
draw
, and
draw
![]() perpendicular to
perpendicular to ![]() and let
and let ![]() intersect
intersect ![]() at
at ![]() . Then
. Then ![]() is a
right angle, since the other angles of the quadrilateral
is a
right angle, since the other angles of the quadrilateral ![]() are right
angles.
Similarly angle
are right
angles.
Similarly angle ![]() is a right angle. Thus
is a right angle. Thus ![]() is a rectangle so
is a rectangle so ![]() and
similarly
and
similarly ![]() is a rectangle and
is a rectangle and ![]() . Moreover
. Moreover ![]() and
and ![]() are
perpendicular since
are
perpendicular since ![]() and
and ![]() . Thus the region labeled
. Thus the region labeled
![]() is a square with side
is a square with side ![]() and the region labeled
and the region labeled ![]() is a square with side
is a square with side
![]() .
.
In figure 2 we have
![]() , and hence
, and hence
Although the theorem we just proved is named for Pythagoras (fl. 530-510 B.C) , it was probably known much earlier. There is evidence that it was known to the Babylonians circa 1000 BC[27, pp 118-121]. Legend has it that
Emperor Yu[circa 21st century B.C.] quells floods, he deepens rivers and streams, observes the shape of mountains and valleys, surveys the high and low places, relieves the greatest calamities and saves the people from danger. He leads the floods east into the sea and ensures no flooding or drowning. This is made possible because of the Gougu theorem[47, page 29].
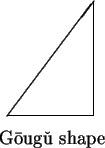
``Gougu'' is the shape shown in the figure, and the Gougu
theorem is our Pythagorean theorem. The prose style here is similar to
that of current day mathematicians trying to get congress to allocate
funds for the support of mathematics.
Katyayana(c. 600 BC or 500BC??) stated the general theorem:
The rope [stretched along the length] of the diagonal of a rectangle makes an [area] which the vertical and horizontal sides make together.[27, page 229]
Proof: Draw the vertical line through
![]() and the horizontal
line through
and the horizontal
line through
![]() . These lines intersect at the point
. These lines intersect at the point
![]() . The
length of
. The
length of
![]() is
is ![]() and the length of
and the length of
![]() is
is ![]() and
and
![]() is the hypotenuse of a right angle with legs
is the hypotenuse of a right angle with legs
![]() and
and
![]() .
.
By the Pythagorean theorem,
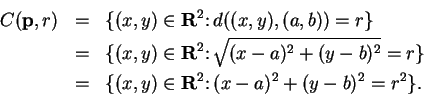
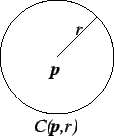
We will now review the method for solving quadratic equations.
If ![]() , then the equation
, then the equation
![]() has no solutions in R.
has no solutions in R.
If
![]() , then the set of solutions of the equation
, then the set of solutions of the equation
![]() is
is
Proof:
Let
![]() be real numbers with
be real numbers with ![]() . Let
. Let
![]() . Then
. Then