Next: 5.3 Monotonic Functions
Up: 5. Area
Previous: 5.1 Basic Assumptions about
Index
5.2 Further Assumptions About Area
In this section we will introduce some more assumptions about area.
The assumptions in this section can actually be proved on the
basis of the basic assumptions we have already made, and in fact
the proofs are easy (the proofs are given in appendix B).
The reason I have made assumptions out of them is that they are
as intuitively plausible as the assumptions I have already made,
and I do not have time to do everything I want to do. I am omitting
the proofs with regret because I agree with Aristotle
that
It is manifest that it is far better to make the principles finite
in number. Nay, they should be the fewest possible provided
they enable all the same results to be proved. This is what
mathematicians insist upon; for they take as principles things
finite either in kind or in number.[25, page 178]
5.14
Assumption (Addition rule for area.)
For any bounded sets
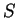
and
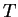
in
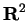
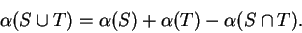 |
(5.15) |
and consequently
5.16
Assumption (Subadditivity of area.)
Let
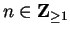
, and let
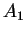
,
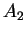
,
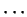
,
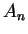
be bounded sets in
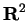
. Then
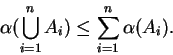 |
(5.17) |
5.18
Assumption (Monotonicity of area.)
Let
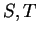
be bounded sets such that
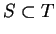
. Then
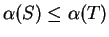
.
5.19
Definition (Zero-area set.)
We
will call a set with zero area a
zero-area
set.
From the normalization property it follows that every horizontal or vertical
segment
has area equal to 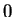 . Thus every horizontal or vertical segment is a zero-area
set.
. Thus every horizontal or vertical segment is a zero-area
set.
5.20
Corollary (to assumption 5.18.) 5.1Every subset of a zero-area set is a zero-area set. In particular the empty
set is
a zero-area set.
5.21
Corollary (to assumption 5.16.) The union of a finite number of zero-area sets is a zero-area set.
5.22
Definition (Almost disjoint.)
We will say that two bounded subsets
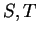
of
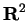
are
almost disjoint if
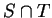
is a zero-area set.
5.23
Examples.
If
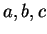
are real numbers with
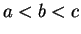
, then since
the boxes
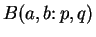
and
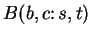
are almost disjoint.
Any zero-area set is almost disjoint from every set - including itself.
5.24
Assumption (Additivity for almost disjoint sets.)
Let
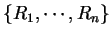
be a finite
set of
bounded sets such that
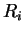
and
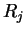
are almost disjoint whenever
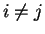
.
Then
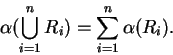 |
(5.25) |
5.26
Notation (Area functions 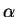 or
or area
)
Any real valued function
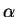
, whose domain is
the family of bounded subsets of
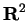
, and which satisfies all of
the assumptions listed in sections
5.1 and
5.2 will
be called an
area function. In these notes I will use the
names ``
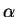
'' and ``area'' to denote area function.
Thus




Next: 5.3 Monotonic Functions
Up: 5. Area
Previous: 5.1 Basic Assumptions about
Index
Ray Mayer
2007-09-07
![]() . Thus every horizontal or vertical segment is a zero-area
set.
. Thus every horizontal or vertical segment is a zero-area
set.