2.6
In this section we will find the areas of two rather complicated
sets, called the inner snowflake and the outer snowflake.
To construct the inner snowflake, we first construct a family of
polygons ![]() ,
, ![]() ,
, ![]() as follows:
as follows:
![]() is an equilateral triangle.
is an equilateral triangle.
![]() is obtained from
is obtained from ![]() by adding an equilateral triangle to the
middle third of each side of
by adding an equilateral triangle to the
middle third of each side of ![]() ,
(see the snowflake figures ).
,
(see the snowflake figures ).
![]() is obtained from
is obtained from ![]() by adding an equilateral triangle to the
middle third of each side of
by adding an equilateral triangle to the
middle third of each side of ![]() , and in general
, and in general
![]() is obtained from
is obtained from ![]() by adding an equilateral triangle to the
middle third of each side of
by adding an equilateral triangle to the
middle third of each side of ![]() .
.
The inner snowflake is the set
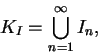
To construct the outer snowflake, we first construct a family of
polygons ![]() ,
, ![]() ,
, ![]() as follows:
as follows:
![]() is a regular hexagon.
is a regular hexagon.
![]() is obtained from
is obtained from ![]() by removing an equilateral triangle from the
middle third of each side of
by removing an equilateral triangle from the
middle third of each side of ![]() ,
(see the snowflake figures ),
,
(see the snowflake figures ),
![]() is obtained from
is obtained from ![]() by removing an equilateral triangle from the
middle third of each side of
by removing an equilateral triangle from the
middle third of each side of ![]() , and in general
, and in general
![]() is obtained from
is obtained from ![]() by removing an equilateral triangle from the
middle third of each side of
by removing an equilateral triangle from the
middle third of each side of ![]() .
.
The outer snowflake is the set
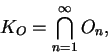
An isosceles 120![]() triangle is an isosceles triangle having a vertex
angle of 120
triangle is an isosceles triangle having a vertex
angle of 120![]() . Since the sum of the angles of a triangle is two right
angles,
the base angles of such a triangle will be
. Since the sum of the angles of a triangle is two right
angles,
the base angles of such a triangle will be
 .
.
The following two technical lemmas2.2 guarantee that
in the process of building ![]() from
from ![]() we never reach a situation
where two of the added triangles intersect each other, or where
one of the added triangles intersects
we never reach a situation
where two of the added triangles intersect each other, or where
one of the added triangles intersects ![]() , and in the process
of building
, and in the process
of building ![]() from
from ![]() we never reach a situation
where two of the removed triangles intersect each other, or where
one of the removed triangles fails to lie inside
we never reach a situation
where two of the removed triangles intersect each other, or where
one of the removed triangles fails to lie inside ![]() .
.
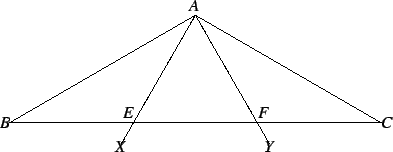
Proof: Let ![]() be an isosceles triangle with
be an isosceles triangle with
![]() . Construct
. Construct ![]() angles
angles ![]() and
and ![]() as shown in the
figure, and let
as shown in the
figure, and let ![]() and
and ![]() denote the points where the lines
denote the points where the lines ![]() and
and ![]() intersect
intersect ![]() . Then since the sum of the angles of a triangle is two right
angles, we have
. Then since the sum of the angles of a triangle is two right
angles, we have
Now suppose we begin with the isosceles ![]() triangle
triangle ![]() with angle
with angle ![]() , and we let
, and we let ![]() be the points that trisect
be the points that trisect ![]() .
Since
.
Since ![]() and
and ![]() determine a unique line, it follows from the previous
discussion that
determine a unique line, it follows from the previous
discussion that ![]() makes a
makes a ![]() angle with
angle with ![]() and
and ![]() makes a
makes a
![]() angle with
angle with ![]() , and that all the conclusions stated in the lemma
are valid.
, and that all the conclusions stated in the lemma
are valid. ![]()
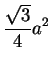 . If
. If
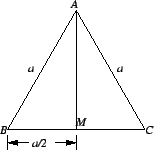
Proof: Let
![]() be an equilateral triangle with side of
length
be an equilateral triangle with side of
length ![]() , and let
, and let ![]() be the midpoint of
be the midpoint of ![]() . Then the altitude of
. Then the altitude of ![]() is
is
![]() , and by the Pythagorean theorem
, and by the Pythagorean theorem
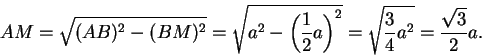
Hence

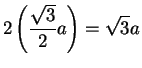 .
.
We now construct two sequences of polygons.
![]() ,
and
,
and
![]() such that
such that
Our general procedure for constructing polygons will be:
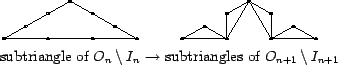
![]() is
constructed from
is
constructed from ![]() by removing an equilateral triangle from the middle
third of each side of
by removing an equilateral triangle from the middle
third of each side of ![]() , and
, and ![]() is constructed from
is constructed from ![]() by adding
an equilateral triangle to the middle third of each side of
by adding
an equilateral triangle to the middle third of each side of ![]() . For each
. For each
![]() ,
,
![]() will consist of a family of congruent isosceles
will consist of a family of congruent isosceles
![]() triangles and
triangles and
![]() is obtained
from
is obtained
from
![]() by removing an equilateral triangle from the middle third of
each side of each isosceles
by removing an equilateral triangle from the middle third of
each side of each isosceles ![]() triangle. Pictures of
triangle. Pictures of ![]() ,
, ![]() , and
, and
![]() are given in the above
snowflake figures). Details of these pictures
are shown below.
are given in the above
snowflake figures). Details of these pictures
are shown below.
Lemma 2.38 guarantees that this process always leads from a set of
isosceles ![]() triangles to a new set of isosceles
triangles to a new set of isosceles ![]() triangles. Note that every vertex of
triangles. Note that every vertex of ![]() is a vertex of
is a vertex of ![]() and of
and of
![]() , and every vertex of
, and every vertex of ![]() is a vertex of
is a vertex of ![]() and of
and of ![]() .
.
Let

The following table
summarizes the values of ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() and
and ![]() :
:
![\begin{displaymath}\begin{array}{\vert l\vert l\vert l\vert l\vert l\vert l\vert...
...4\over 9}\right)^{n-2}
{A_1\over 9}
[2ex] \hline
\end{array}\end{displaymath}](img500.gif)
By the formula for a finite geometric series we have
![\begin{displaymath}1+{4\over 9}+({4\over 9})+\cdots +({4\over 9})^{n-1}={{1-({4\...
...}\over
{1-{4\over 9}}}={9\over 5}\left[1-({4\over 9})^n\right].\end{displaymath}](img519.gif)
By using this result in equations (2.40) and (2.41) we obtain
![$\displaystyle a_{n+1}= a_1 + {a_1 \over 3} \cdot{9 \over 5}
\left[ 1-\left({4\over 9}\right)^n\right]$](img524.gif) |
|||
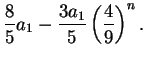 |
Now you can show that
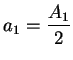 , so the last equation may be
written as
, so the last equation may be
written as
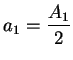 , i.e. show that
, i.e. show that
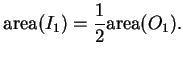
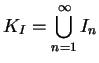 and
and
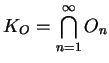 .
Here the infinite union
.
Here the infinite union
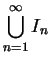 means the set of all points
means the set of all points 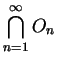 means the set of points
means the set of points
For all ![]() in
in
![]() , we have
, we have
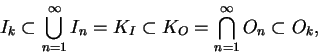
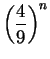 can be made very small by taking
can be made very small by taking
Note that both snowflakes touch the boundary of the circumscribed hexagon in infinitely many points.
It is natural to ask whether the sets ![]() and
and ![]() are the same.
are the same.
The snowflakes were discovered by Helge von
Koch(1870-1924), who published his results in
1906 [31]. Actually Koch was not interested in the snowflakes as
two-dimensional objects, but as one-dimensional curves. He considered only
part of the boundary of the regions we have described. He showed that the
boundary of ![]() and
and ![]() is a curve that does not have a tangent at any
point. You should think about the question: ``In what sense is the boundary of
is a curve that does not have a tangent at any
point. You should think about the question: ``In what sense is the boundary of
![]() a curve?'' In order to answer this question you would need to answer the
questions ``what is a curve?'' and ``what is the boundary of
a set in
a curve?'' In order to answer this question you would need to answer the
questions ``what is a curve?'' and ``what is the boundary of
a set in
![]() ?''
We will not consider these questions in this course, but you might
want to think about them.
?''
We will not consider these questions in this course, but you might
want to think about them.
I will leave the problem of calculating the perimeter of a snowflake as an exercise. It is considerably easier than finding the area.
What do you think the perimeter of ![]() should be? (Since it isn't really
clear what we mean by ``the perimeter of
should be? (Since it isn't really
clear what we mean by ``the perimeter of ![]() ,'' this question doesn't really
have a ``correct'' answer - but you should come up with some answer.)
,'' this question doesn't really
have a ``correct'' answer - but you should come up with some answer.)