In this section we will discuss a Maple program for calculating approximate
values
of ![]() for monotonic functions
for monotonic functions ![]() on the interval
on the interval ![]() .
The programs will be
based on formulas discussed in theorem 5.40.
.
The programs will be
based on formulas discussed in theorem 5.40.
Let ![]() be a decreasing function from the interval
be a decreasing function from the interval ![]() to
to
![]() ,
and let
,
and let
![]() be a partition of
be a partition of ![]() .
We know that
.
We know that
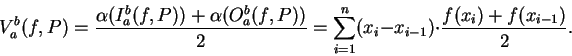
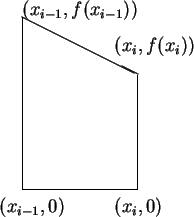
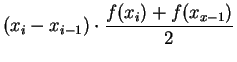 represents
the area of the trapezoid with vertices
represents
the area of the trapezoid with vertices
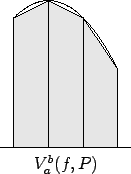
In the programs below, leftsum(f,a,b,n) calculates
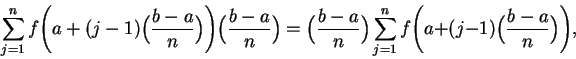
rightsum(f,a,b,n) calculates
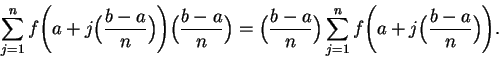
average(f,a,b,n) calculates the average of
leftsum(f,a,b,n) and rightsum(f,a,b,n).
The
equation of the unit circle is ![]() , so the upper unit semicircle is the
graph of
, so the upper unit semicircle is the
graph of ![]() where
where
![]() . The area of the unit circle is 4 times
the area of the portion of the circle in the first quadrant, so
. The area of the unit circle is 4 times
the area of the portion of the circle in the first quadrant, so
My routines and calculations are given below. Here leftsum,
rightsum and average are all
procedures with four arguments, f,a,b, and n.
f is a function.
a and b are the endpoints of an interval.
n is the number of subintervals in a partition of [a,b].
The functions F and G are defined by
F![]() and
and G
![]() .
The command
.
The command
average(F,1.,2.,10000);
estimates
4*average(G,0.,1.,2000);
estimates
> leftsum := > (f,a,b,n) -> (b-a)/n*sum(f( a +((j-1)*(b-a))/n),j=1..n);
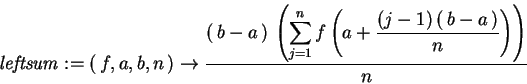
> rightsum := > (f,a,b,n) -> (b-a)/n*sum(f( a +(j*(b-a))/n),j=1..n);
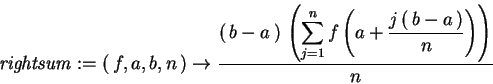
> average := > (f,a,b,n) -> (leftsum(f,a,b,n) + rightsum(f,a,b,n))/2;
> F := t -> 1/t;
> leftsum(F,1.,2.,10000);
> rightsum(F,1.,2.,10000);
> average(F,1.,2.,10000);
> ln(2.);
> G := t -> sqrt(1-t^2);
> 4*leftsum(G,0.,1.,2000);
> 4*rightsum(G,0.,1.,2000);
> 4*average(G,0.,1.,2000);
> evalf(Pi);
Observe that in these examples, average yields
much more accurate approximations than either leftsum
or rightsum.