



Next: A Associativity
Up: Numbers
Previous: Bibliography
Index
- Exercise 2.11:
- In each case there is only one invertible element.
- Exercise 2.40:
- Note that the calculator sum of a very small number and a very large number is the large number. Note that the calculator product of two small positive numbers is 0.
- Exercise 2.55:
- The system
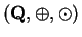 fails two axioms. The other three each fail one axiom.
fails two axioms. The other three each fail one axiom.
- Exercise 2.78:
- Use (2.75).
- Exercise 2.90:
- For part (b), use (2.74).
- Exercise 2.93:
- Part e) can be done quickly by using parts a), b) and d).
- Exercise 2.123:
- One of the conditions is that
 and
and 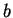 have the same sign.
have the same sign.
- Exercise 2.135:
- There are nine cases to consider (three for
 and three for
and three for 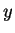 ). They can be reduced to five cases, one of which is (
). They can be reduced to five cases, one of which is (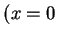 or
or 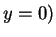 .
.
- Exercise 2.144:
- There is a very short proof for a).
- Exercise 2.145:
- Apply the product formula for absolute values to
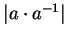 .
.
- Exercise 2.154:
- Use (2.138).
- Exercise 3.24:
- You can take
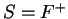 .
.
- Exercise 3.32:
- Suppose
 is both even and odd, and derive a contradiction by using theorems 3.15 and 3.19.
is both even and odd, and derive a contradiction by using theorems 3.15 and 3.19.
- Exercise 3.43:
- For part b) use part a) together with exercise 3.32
- Exercise 3.57:
- You can let
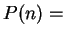 ``
``
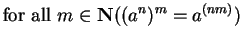 '' or
'' or
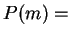 ``
``
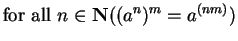 ''.
''.
- Exercise 3.82:
- f) Note that
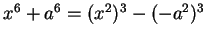 .
.
- Exercise 3.84:
-
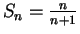 .
.
- Exercise 3.86:
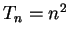 .
.
- Exercise 4.19:
- a) Note that
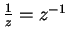 . b) The solutions are
. b) The solutions are 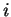 and
and
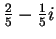 .
.
- Exercise 4.23:
- For part c), write
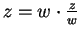 and use part b). Remark 4.22 is used for part f).
and use part b). Remark 4.22 is used for part f).
- Exercise 4.25:
- a) 1. b) 32i.
- Exercise 5.15:
- I let
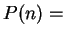 ``
``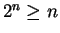 and
and 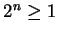 '' and I used the fact that
'' and I used the fact that
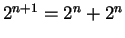 . (It would be reasonable to assume
. (It would be reasonable to assume 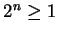 for all
for all  , but I proved it).
, but I proved it).
- Exercise 5.48:
- Suppose
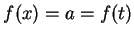 , and use trichotomy to show that
, and use trichotomy to show that 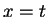 .
.
- Exercise 5.51:
- a) If
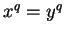 , then
, then 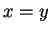 . b) If
. b) If
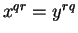 , then
, then 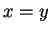 . (We know the laws of exponents for integer exponents.)
. (We know the laws of exponents for integer exponents.)
- Exercise 5.54:
- Raise both sides of the equation to the same integer power, and use laws of exponents for integer powers.
- Exercise 6.5:
- e) Notice that
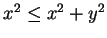 , and use theorem 2.128.
, and use theorem 2.128.
- Exercise 6.26:
- The roots are
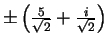 .
.
- Exercise 7.21:
- I showed
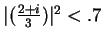 , so that
, so that
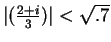 . Then I used the fact that
. Then I used the fact that 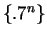 is known to be a null sequence, and used the root theorem and the comparison theorem.
is known to be a null sequence, and used the root theorem and the comparison theorem.
- Exercise 7.22:
- All three sequences are null sequences. For the last sequence, I showed
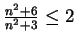 for all
for all 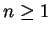 . For the first sequence
. For the first sequence 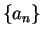 , I showed
, I showed
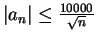 for all
for all 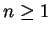 .
.
- Exercise 7.24:
- The set of all complex sequences does not form a field. All of the field axioms except one hold.
- Exercise 7.28:
-
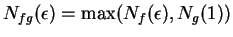 works.
works.
- Exercise 7.44:
- You can take
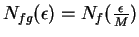 , where
, where 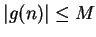 for all
for all
 .
.
- Exercise 7.49:
- Note that
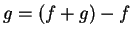 , and show that the assumption
, and show that the assumption 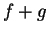 converges is contradictory.
converges is contradictory.
- Exercise 7.50:
- Note that if
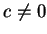 , then
, then
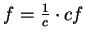 .
.
- Exercise 7.56:
- Multiply numerator and denominator of
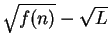 by
by
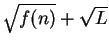 .
.
- Exercise 7.57:
- All of the sequences converge.
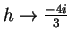 and
and
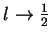 .
.
- Exercise 7.58:
- If
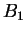 is a bound for
is a bound for  , and
, and 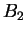 is a bound for
is a bound for  , then
, then 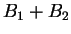 is a bound for
is a bound for 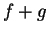 .
.
- Exercise 7.60:
- A convergent sequence is the sum of a null sequence and a constant sequence. Now use exercise 7.58.
- Exercise 7.69:
-
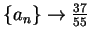 .
.
- Exercise 7.70:
- One of the sequences diverges. One of the limits is
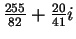 .
.
- Exercise 7.74:
- Apply theorem 7.7 to
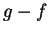 .
.
- Exercise 7.75:
- The statement is false.
- Exercise 7.86:
- The sequence converges to
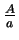 or to
or to 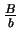 or else it diverges. (You should find exact conditions on
or else it diverges. (You should find exact conditions on  ,
, 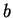 ,
, 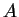 , and
, and 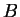 corresponding to each case.)
corresponding to each case.)
- Exercise 7.94:
- If
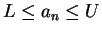 for all
for all
 , then either
, then either 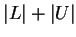 or
or 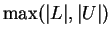 will be a bound for
will be a bound for 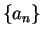
- Exercise 7.100:
- Use corollary 7.96 to show that the sequence converges. Note
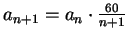 . Use the translation theorem to show that the limit is
. Use the translation theorem to show that the limit is 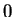 .
.
- Exercise 8.4:
- I used the polar decomposition for
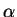 .
.
- Exercise 8.19:
- Yes. In fact every function from
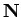 to
to
 is continuous. The only integer
is continuous. The only integer 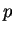 that satisfies
that satisfies
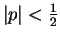 is zero.
is zero.
- Exercise 8.43:
- a) Limit does not exist. b) Let
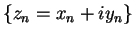 be a sequence converging to
be a sequence converging to 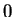 . Apply null-times-bounded theorem to
. Apply null-times-bounded theorem to 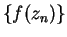 . c) I looked at sequences
. c) I looked at sequences
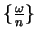 , where
, where 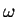 is a direction.
is a direction.
- Exercise 9.10:
- Four of the requested five functions exist. The other one doesn't.
- Exercise 9.13:
- Apply theorem 9.11 to
 , where
, where
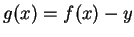
- Exercise 9.17:
- All four functions exist. I described
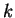 by drawing its graph.
by drawing its graph.
- Exercise 9.19:
- Assume
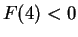 and derive a contradiction from the intermediate value theorem.
and derive a contradiction from the intermediate value theorem.
- Exercise 10.10:
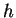 is nowhere differentiable. The same sequences that show complex conjugation is nowhere differentiable show that
is nowhere differentiable. The same sequences that show complex conjugation is nowhere differentiable show that 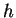 is also.
is also.
- Exercise 10.17:
-
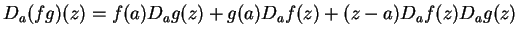 .
.
- Exercise 10.19:
- Write
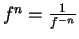 , and use the reciprocal rule and exercise 10.18.
, and use the reciprocal rule and exercise 10.18.
- Exercise 10.20:
- Use the product rule and the reciprocal rule.
- Exercise 10.31:
- Only one of the three statements is true.
- Exercise 10.37:
- Use the result of exercise 6.36
- Exercise 10.50:
- For both parts, compare with
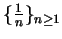
- Exercise 10.51:
- The exact value of
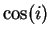 is
is
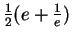 . You can't prove this (because we have not yet defined
. You can't prove this (because we have not yet defined 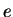 ), but you can check your answer using this.
), but you can check your answer using this.
- Exercise 11.19:
- c) Note that the comparison test holds only for sequences of non-negative numbers.
- Exercise 11.28:
- In most cases there is one value for which the ratio test gives no information. However the exceptional values are usually standard test series. For part g) the exceptional value was considered in example 11.27.
- Exercise 11.48:
- b) Show that the real and imaginary parts of the series both converge.
- Exercise 11.49:
- Both series converge absolutely for
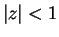 and diverge for
and diverge for 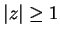 . (I used the ratio test.)
. (I used the ratio test.)
- Exercise 12.6:
- a) If
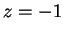 then
then 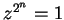 for all
for all 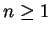 , and if
, and if 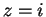 , then
, then 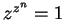 for all
for all 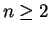 . Except for the first few terms, both series are geometric series,
. Except for the first few terms, both series are geometric series,
- Exercise 12.14:
- a) Consider geometric series of the form
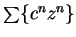 . c) Cf exercise 12.5.a
. c) Cf exercise 12.5.a
- Exercise 12.20:
- The sums are
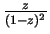 and
and
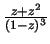 Get the second by differentiating the first.
Get the second by differentiating the first.
- Exercise 12.33:
- a) Use induction and (12.29). b) Use part a) and (12.28).
- Exercise 12.34:
- Calculate
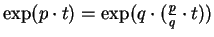 using exercise 12.33
using exercise 12.33
- Exercise 12.42:
- a) Write
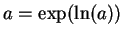 and use (12.28). b) Write
and use (12.28). b) Write
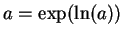 and use exercise 12.34.
and use exercise 12.34.
- Exercise 12.51:
- Write the trig functions in terms of exponentials, and use
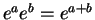 several times.
several times.
- Exercise 12.59:
- Everything follows from
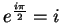 and
and
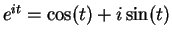 and
and
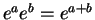 .
.
- Exercise 12.70:
-
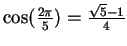 .
.




Next: A Associativity
Up: Numbers
Previous: Bibliography
Index