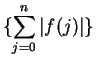 converges. In this case, we also say that the series
converges. In this case, we also say that the series
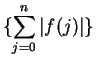 converges. In this case, we also say that the series
converges. In this case, we also say that the series
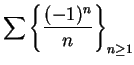 is
convergent, but is not absolutely convergent.
is
convergent, but is not absolutely convergent.
Proof:
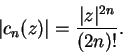
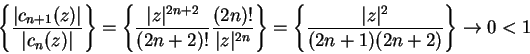
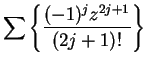 is also convergent for all
is also convergent for all
Motivated by the results of section 10.3, we make the following definitions:
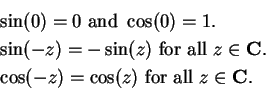
For all
![]() ,
,
![]() , let
, let
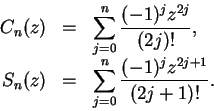
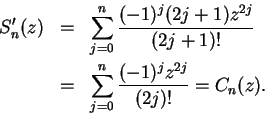
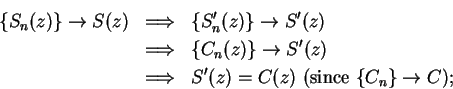
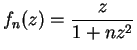 for all
for all
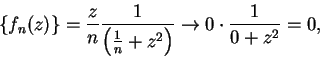
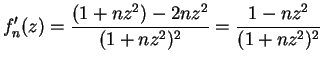 . So
. So
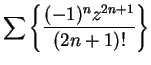 converges for all
converges for all
The ratio test was stated by Jean D'Alembert in 1768, and by Edward Waring in 1776[31, p 465]. D'Alembert knew that the ratio test guaranteed absolute convergence.
The alternating series test appears in a letter from Leibniz to Jacob Bernoulli written in 1713[31, p461].
The series (11.35) for ![]() is called Mercator's formula after Nicolaus Mercator
who published it in 1668. It was discovered earlier by Newton in 1664
when he was an
undergraduate at Cambridge. After Newton read Mercator's book, he quickly wrote down
some of his own ideas (which were much more general than Mercator's) and allowed his
notes to be circulated, but not published. Newton used the logarithm formula to
calculate
is called Mercator's formula after Nicolaus Mercator
who published it in 1668. It was discovered earlier by Newton in 1664
when he was an
undergraduate at Cambridge. After Newton read Mercator's book, he quickly wrote down
some of his own ideas (which were much more general than Mercator's) and allowed his
notes to be circulated, but not published. Newton used the logarithm formula to
calculate ![]() to 68 decimals (of which the 28th and 43rd were wrong), but a
few years later, he redid the calculation and corrected the errors.
to 68 decimals (of which the 28th and 43rd were wrong), but a
few years later, he redid the calculation and corrected the errors.
See [22, chapter 2] for a discussion of Newton's work on series.
The series representation for ![]() (11.37) is called Gregory's
formula after John Gregory (1638-1675) or Leibniz's formula after Gottfried
Leibniz (1646-1716). However, it was known to sixteenth century Indian
mathematicians who credited it to Madhava (c. 1340-1425). The Indian version was
(11.37) is called Gregory's
formula after John Gregory (1638-1675) or Leibniz's formula after Gottfried
Leibniz (1646-1716). However, it was known to sixteenth century Indian
mathematicians who credited it to Madhava (c. 1340-1425). The Indian version was