



Next: 11.4 Absolute Convergence
Up: 11. Infinite Series
Previous: 11.2 Convergence Tests
Index
11.29
Definition (Alternating series.)
Series of the form
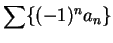
or
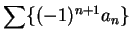
where
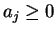
for all
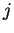
are called
alternating series.
11.30
Theorem (Alternating series test.)
Let  be a decreasing sequence of positive numbers such that
be a decreasing sequence of positive numbers such that 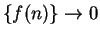 . Then
. Then
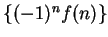 is summable. Moreover,
and
for all
is summable. Moreover,
and
for all
 .
.
Proof: Let
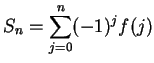 . For all
. For all
 ,
,
and
Thus 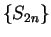 is decreasing and
is decreasing and 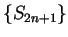 is increasing. Also, for all
is increasing. Also, for all
 ,
,
so 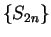 is bounded below by
is bounded below by 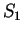 , and
, and
so 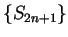 is bounded above by
is bounded above by 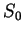 .
.
It follows that there exist real numbers 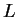 and
and 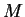 such that
such that
Now
so 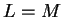 .
.
It follows from the next lemma that 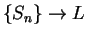 ; i.e.,
; i.e.,
Since for all

we have
and since
Thus, in all cases,
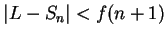 ; i.e.,
; i.e.,
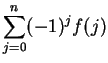 approximates
approximates
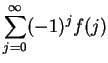 with an error of no more than
with an error of no more than
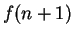 .
.

11.31
Lemma.
Let 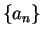 be a real sequence and let
be a real sequence and let
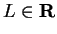 . Suppose
. Suppose
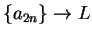 and
and
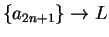 . Then
. Then 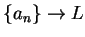 .
.
Proof: Let 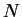 be a precision function for
be a precision function for 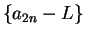 and let
and let 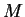 be a precision
function for
be a precision
function for
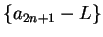 . For all
. For all
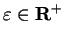 , define
, define
I claim
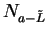 is a precision function for
is a precision function for 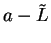 , and hence
, and hence 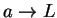 .
Let
.
Let
 .
.
- Case 1:
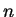 is even. Suppose
is even. Suppose 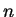 is even.
Say
is even.
Say 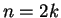 where
where
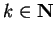 . Then
. Then
- Case 2:
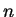 is odd.
Suppose
is odd.
Suppose 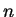 is odd. Say
is odd. Say 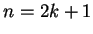 where
where
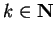 .
Then
.
Then
Hence, in all cases,
11.32
Remark.
The alternating series test has obvious generalizations for series such as
and we will use these generalizations.
11.33
Example.
If
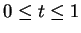
, then
are decreasing positive null sequences, so
are summable; i.e.,
(These are the sequences we called
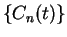
and
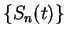
in example
10.3.)
Also,
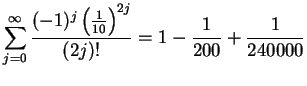 ,
with an error smaller than
,
with an error smaller than
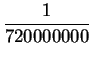 . My calculator says
. My calculator says
and
11.34
Entertainment.
Since
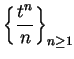
is a decreasing positive null
sequence for
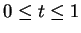
, it follows that
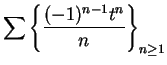
converges for
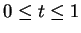
. We will now explicitly
calculate the limit of this series using a few ideas that are not justified by results
proved in this course. We know that for all
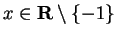
, and all

,
Hence, for all
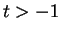
,
i.e.,
Thus
Hence
for all
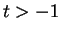
.
If we can show that
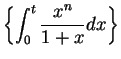 is a null
sequence, it follows that
is a null
sequence, it follows that
or in other words,
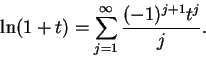 |
(11.35) |
I claim
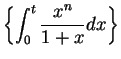
is a null sequence for
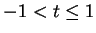
and hence (
11.35) holds for
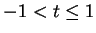
. In particular,
First suppose
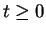
, then
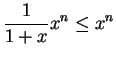
for
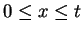
, so
Since
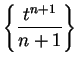
is a null sequence for
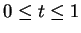
, it follows from the comparison test that
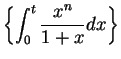
is a null sequence for
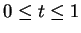
.
Now suppose
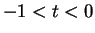
. Then
so
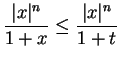
and
If
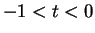
, then
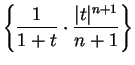
is a
null sequence, so
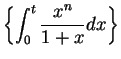
is a null
sequence.

11.36
Entertainment.
By starting with the formula
for all
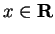
and using the ideas from the last example, show that
![\begin{displaymath}
\sum_{j=0}^\infty {{(-1)^jx^{2j+1}}\over {(2j+1)}}=\arctan(x)\mbox{ for all }x\in[-1,1].
\end{displaymath}](img1599.gif) |
(11.37) |
Conclude that




Next: 11.4 Absolute Convergence
Up: 11. Infinite Series
Previous: 11.2 Convergence Tests
Index
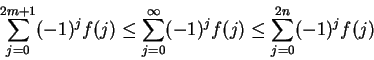
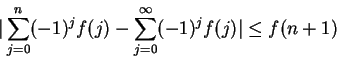
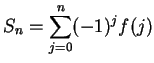 . For all
. For all
![]() ,
,
![]() and
and ![]() such that
such that
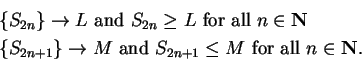
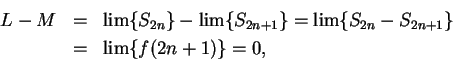
![]() ; i.e.,
; i.e.,
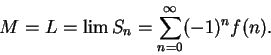
![]()
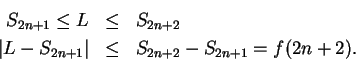
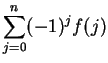 approximates
approximates
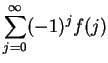 with an error of no more than
with an error of no more than
![]() be a precision function for
be a precision function for ![]() and let
and let ![]() be a precision
function for
be a precision
function for
![]() . For all
. For all
![]() , define
, define
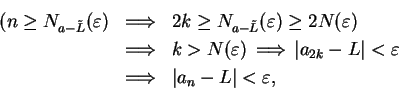
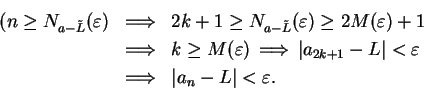
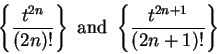
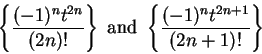
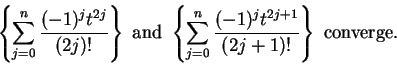
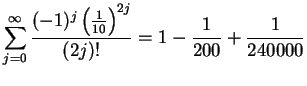 ,
with an error smaller than
,
with an error smaller than
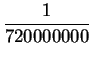 . My calculator says
. My calculator says
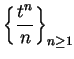 is a decreasing positive null
sequence for
is a decreasing positive null
sequence for 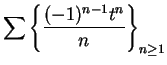 converges for
converges for 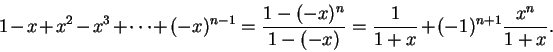
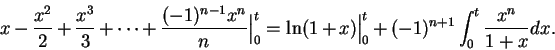
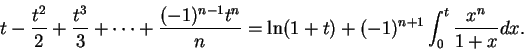
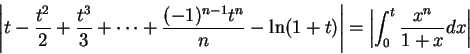
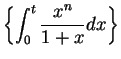 is a null
sequence, it follows that
is a null
sequence, it follows that
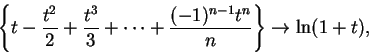
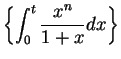 is a null sequence for
is a null sequence for
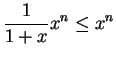 for
for 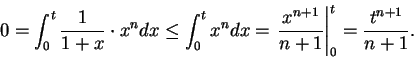
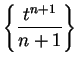 is a null sequence for
is a null sequence for 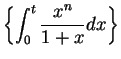 is a null sequence for
is a null sequence for 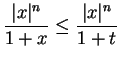 and
and
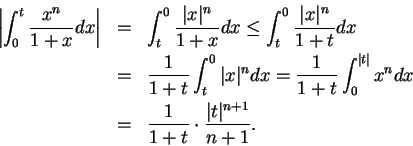
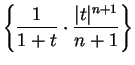 is a
null sequence, so
is a
null sequence, so
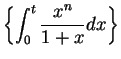 is a null
sequence.
is a null
sequence.
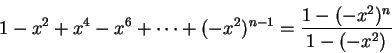
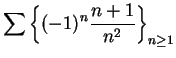
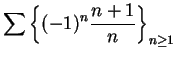
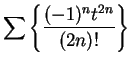 (assume here
(assume here