Next: 11. Infinite Series
Up: 10. The Derivative
Previous: 10.2 Differentiable Functions on
Index
10.3 Trigonometric Functions
10.45
Example.
Suppose that there are real valued functions
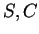
on

such that
You have seen such functions in your previous calculus course. Let
.
Then
Hence,
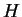
is constant on

, and since
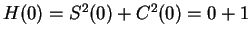
, we have
In particular,
Let
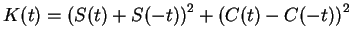 .
By the power rule and chain rule,
.
By the power rule and chain rule,
Hence
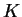
is constant and since
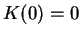
, we conclude
that
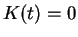
for all
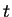
.
Since a sum of squares in

is zero only when
each summand is zero, we conclude
that
Let
Then
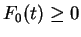
for all
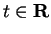
and
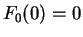
. I will now construct a sequence
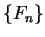
of functions on

such
that
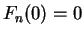
for all

, and
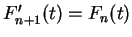
for all
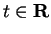
. I have
It should be clear how this pattern continues. Since
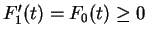
,
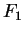
is increasing on
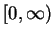
and since
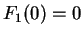
,
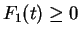
for
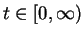
. Since
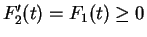
on
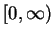
,
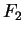
is increasing
on
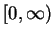
and since
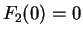
,
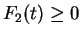
for
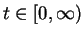
.
This argument continues (I'll omit the inductions), and I conclude that 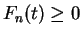 for all
for all
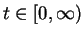 and all
and all
 . Now
. Now
For each

,
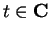
, define
The equations above suggest that for all

,
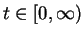
,
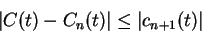 |
(10.46) |
and
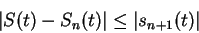 |
(10.47) |
I will not write down the induction proof for this because I believe that it is
clear from the examples how the proof goes, but the notation becomes complicated.
Since 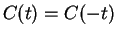 ,
,
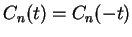 and
and
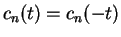 , the relation
(10.46) actually holds for all
, the relation
(10.46) actually holds for all
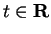 (not just for
(not just for
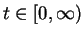 ) and
similarly relation (10.47) holds for all
) and
similarly relation (10.47) holds for all
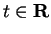 . From (10.46)
and (10.47), we see that if
. From (10.46)
and (10.47), we see that if 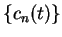 is a null sequence, then the
sequence
is a null sequence, then the
sequence 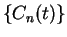 converges to
converges to 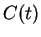 , and if
, and if 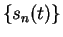 is a null sequence,
then
is a null sequence,
then 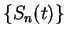 converges to
converges to 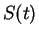 .
.
We will show later that both sequences 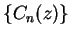 and
and 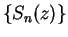 converge for all
complex numbers
converge for all
complex numbers 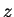 , and we will define
, and we will define
for all
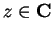
. The discussion above is supposed to convince you that for real
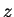
this definition agrees with whatever definition of sine and cosine you are
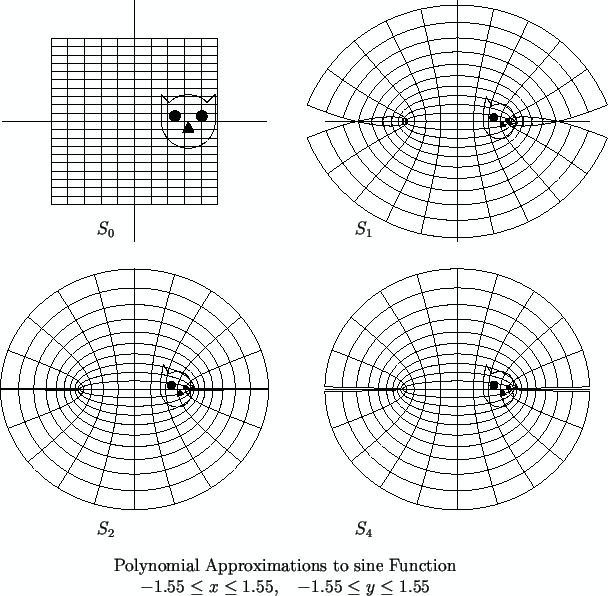
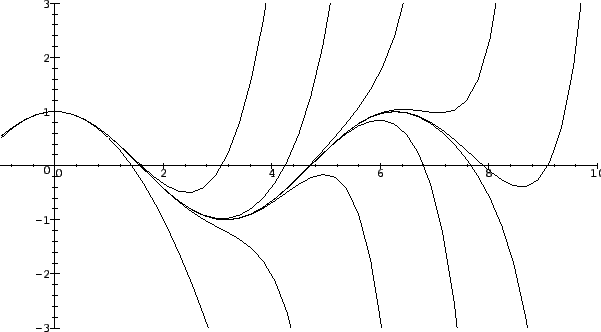
familiar with. The figures show graphs of
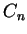
and
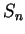
for small
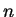
.
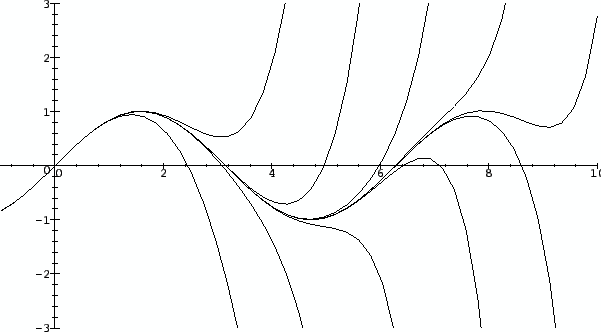
Graphs of the polynomials
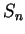
for
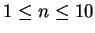
Graphs of the polynomials
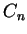
for
10.50
Exercise.
A
Show that
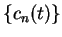
and
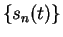
are null sequences for all
complex
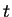
with
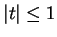
.
10.51
Exercise.
A
a) Using calculator arithmetic, calculate the limits of
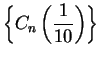
and
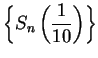
accurate to 8 decimals. Compare
your results with your calculator's value of
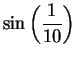
and
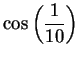
. [Be sure to use radian
mode.]
b) Calculate 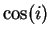 to 3 or 4 decimals accuracy. Note that
to 3 or 4 decimals accuracy. Note that 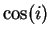 is
real.
is
real.
The figure shows graphical representations for 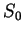 ,
, 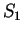 ,
, 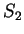 , and
, and 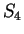 .
Note that
.
Note that 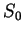 is the identity function.
is the identity function.
10.52
Entertainment.
Show that for all
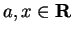
and
Use a trick similar to the trick used to show that 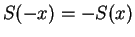 and
and 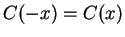 .
.
10.53
Entertainment.
By using the definitions
(
10.48) and (
10.49), show that
a) For all
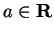 ,
,  is real, and
is real, and
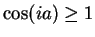 .
.
b) For all
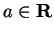 ,
, 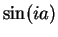 is pure imaginary, and
is pure imaginary, and 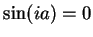 if and
only if
if and
only if 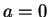 .
.
c) Assuming that the identity
is valid for all complex numbers
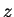
and
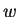
, show that
if
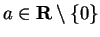
then sin maps the horizontal line
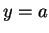
to the ellipse
having the equation
d) Describe where 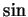 maps vertical lines. (Assume that the identity
maps vertical lines. (Assume that the identity
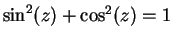 holds for all
holds for all
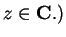
10.54
Note.
Rolle's theorem is named after Michel Rolle (1652-1719).
An English translation of Rolle's
original statement and proof can be found in [
46, pages 253-260].
It takes a considerable effort to see any relation between
what Rolle says, and what our form of his theorem says.
The series representations for sine and cosine (10.48) and
(10.49) are usually credited to Newton, who discovered them some time
around 1669. However, they were known in India centuries before this. Several
sixteenth century Indian writers quote the formulas and attribute them to Madhava of
Sangamagramma (c. 1340-1425)[30, p 294].
The method used for finding the series for sine and cosine
appears in the 1941 book What is Mathematics" by Courant and
Robbins[17, page 474]. I expect that the method
was well known at that time.




Next: 11. Infinite Series
Up: 10. The Derivative
Previous: 10.2 Differentiable Functions on
Index
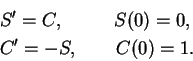
![]() .
By the power rule and chain rule,
.
By the power rule and chain rule,
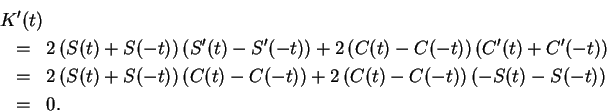
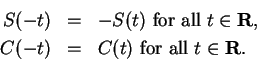
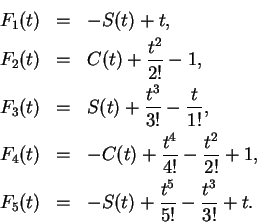
![]() for all
for all
![]() and all
and all
![]() . Now
. Now
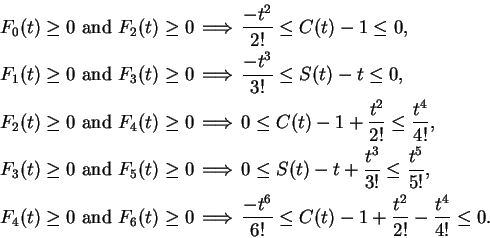
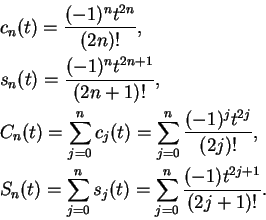
![]() ,
,
![]() and
and
![]() , the relation
(10.46) actually holds for all
, the relation
(10.46) actually holds for all
![]() (not just for
(not just for
![]() ) and
similarly relation (10.47) holds for all
) and
similarly relation (10.47) holds for all
![]() . From (10.46)
and (10.47), we see that if
. From (10.46)
and (10.47), we see that if ![]() is a null sequence, then the
sequence
is a null sequence, then the
sequence ![]() converges to
converges to ![]() , and if
, and if ![]() is a null sequence,
then
is a null sequence,
then ![]() converges to
converges to ![]() .
.
![]() and
and ![]() converge for all
complex numbers
converge for all
complex numbers ![]() , and we will define
, and we will define
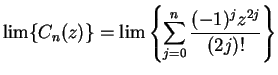
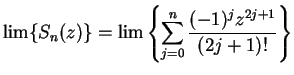

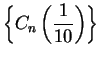 and
and
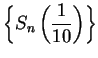 accurate to 8 decimals. Compare
your results with your calculator's value of
accurate to 8 decimals. Compare
your results with your calculator's value of
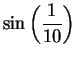 and
and
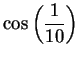 . [Be sure to use radian
mode.]
. [Be sure to use radian
mode.]