



Next: 10.3 Trigonometric Functions
Up: 10. The Derivative
Previous: 10.1 Derivatives of Complex
Index
10.21
Warning.
By the definition of differentiablity
given in Math 111, the domain of a function was required to contain
some interval
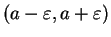
in order for the function be differentiable at

.
In definition
10.1 this condition has been replaced
by requiring

to be a limit point of the domain of the function.
Now a function whose domain is a closed interval
![$[a,b]$](img935.gif)
may be differentiable at

and/or
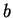
.
10.22
Definition (Critical point.)
Let

be a complex function, and let
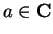
. If

is differentiable at

and
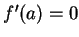
, we call

a
critical point for

.
10.23
Theorem (Critical Point Theorem.)
Let
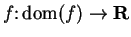 be a function.
Suppose
be a function.
Suppose  has a maximum at some point
has a maximum at some point
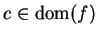 , and that
, and that
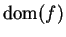 contains an interval
contains an interval
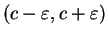 where
where
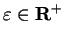 .
If
.
If  is differentiable at
is differentiable at 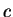 , then
, then 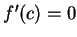 . The theorem also holds if we
replace `` maximum" by `` minimum."
. The theorem also holds if we
replace `` maximum" by `` minimum."
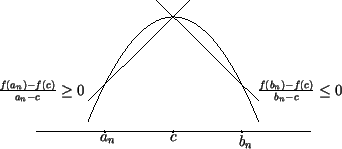
Proof: Suppose  has a maximum at
has a maximum at 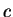 ,
,
Define two sequences 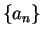 ,
, 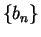 in
in
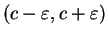 by
by
Clearly 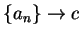 and
and 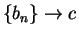 , and
, and
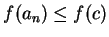 and
and
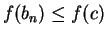 for all
for all
 .
We have
.
We have
By the inequality theorem,
Also,
so
Since
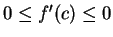 , we conclude that
, we conclude that 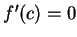 . The proof for minimum points
is left to you.
. The proof for minimum points
is left to you.

10.24
Theorem (Rolle's Theorem.)
Let
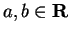 with
with 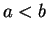 and let
and let
![$f\colon [a,b]\to\mbox{{\bf R}}$](img934.gif) be a function that is
continuous on
be a function that is
continuous on ![$[a,b]$](img935.gif) and differentiable on
and differentiable on 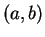 . Suppose that
. Suppose that 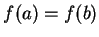 .
Then there is a number
.
Then there is a number 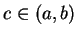 such that
such that 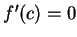 .
.
Proof: We know from the extreme value theorem that  has a maximum at some point
has a maximum at some point
![$p\in [a,b]$](img948.gif) . If
. If 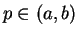 , then the critical point theorem says
, then the critical point theorem says 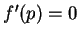 , and we
are finished. Suppose
, and we
are finished. Suppose 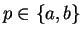 . We know there is a point
. We know there is a point ![$q\in[a,b]$](img1120.gif) such
that
such
that  has a minimum at
has a minimum at 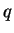 . If
. If 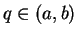 we get
we get 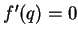 by the critical
point theorem, so suppose
by the critical
point theorem, so suppose 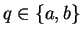 . Then since
. Then since 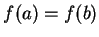 and
and
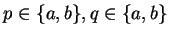 , we have
, we have 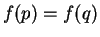 , and it follows that
, and it follows that  is a
constant function on
is a
constant function on ![$[a,b]$](img935.gif) , and in this case
, and in this case 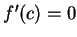 for all
for all 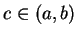 .
.

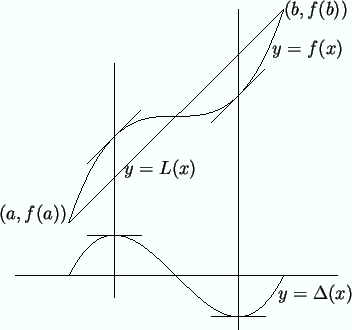
This theorem says that the tangent to the graph of  at some point
at some point
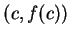 is parallel to the chord joining
is parallel to the chord joining
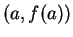 to
to
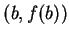 .
.
Proof: Let
so the equation of the line joining
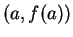 to
to
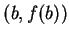 is
is 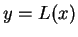 , and
, and
Let
Then
and 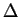 is continuous on
is continuous on ![$[a,b]$](img935.gif) and differentiable on
and differentiable on 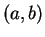 . By Rolle's
theorem, there is some
. By Rolle's
theorem, there is some 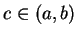 such that
such that 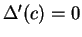 ; i.e.,
; i.e.,
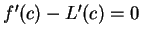 ; i.e.,
; i.e.,
10.26
Remark.
The mean value theorem does not hold for complex valued functions. Let
Then
so
But
so

, and there is no point in
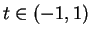
with
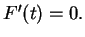
10.27
Definition (Interior point.)
Let
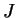
be an interval in

. A number
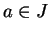
is an
interior point
of
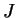
if and only if

is not an end point
of
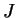
. The set of all interior points of
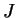
is called the
interior of
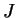
and is denoted by
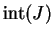
.
10.28
Examples.
If
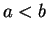
, then
If 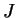 is an interval, and
is an interval, and 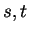 are points in
are points in 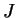 with
with
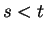 , then every point in
, then every point in 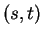 is in the interior of
is in the interior of 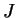 .
.
10.29
Theorem.
Let 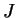 be an interval in
be an interval in
 , and let
, and let
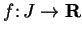 be a continuous
function on
be a continuous
function on 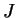 . Then:
. Then:
- a)
- If
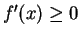 for all
for all
 , then
, then  is increasing on
is increasing on 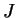 .
.
- b)
- If
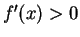 for all
for all
 , then
, then  is strictly increasing on
is strictly increasing on 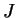 .
.
- c)
- If
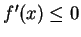 for all
for all
 , then
, then  is decreasing on
is decreasing on 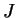 .
.
- d)
- If
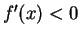 for all
for all
 , then
, then  is strictly decreasing on
is strictly decreasing on 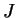 .
.
- e)
- If
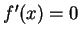 for all
for all
 , then
, then  is constant on
is constant on 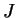 .
.
Proof: All five statements have similar proofs. I'll prove only part a).
Suppose 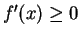 for all
for all
 . Then for all
. Then for all 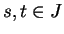 with
with 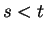 we have
we have  is continuous on
is continuous on ![$[s,t]$](img1162.gif) and differentiable
on
and differentiable
on 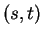 , so by the mean value theorem
, so by the mean value theorem
Hence,  is increasing on
is increasing on 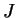 .
.
10.30
Exercise.
Prove part e) of the previous theorem; i.e., show that if
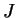
is an interval in

and
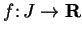
is continuous and satisfies
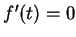
for all
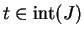
, then

is
constant on
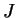
. [It is sufficient to show that
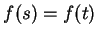
for all
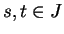
.]
Proof:
Let 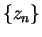 be any sequence in
be any sequence in
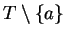 such that
such that
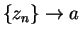 . Then
. Then 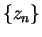 is a sequence in
is a sequence in
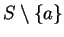 ,
and hence
,
and hence
It follows that
I've shown that
10.33
Definition (Path, line segment.)
If
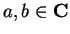
, then the
path joining  to
to 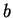
is the function
![$\lambda_{ab}\colon[0,1]\to\mbox{{\bf C}}$](img1185.gif)
and the set
is called the
line segment joining

to
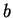
.
10.34
Example.
We showed in example
10.9 that the function
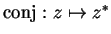
is a nowhere differentiable function on

.
I will show that for all

,
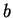
in

with
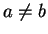
, the restriction
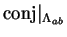
of conj to the line segment
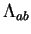
is differentiable,
and
Note that all points of
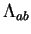
are limit points
of
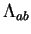
. If
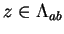
, then for some real number
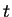
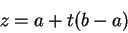 |
(10.35) |
and
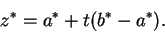 |
(10.36) |
If we solve equation (
10.35) for
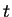
we get
By using this value for
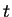
in equation
(
10.36) we get
Let
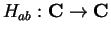
be defined by
Then
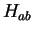
is differentiable, and
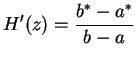
for all
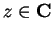
. We have
so by the restriction theorem
10.37
Exercise.
A
Let
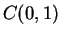
denote the unit circle in

. Show that
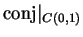
is differentiable, and that
In general, the real and imaginary parts of a differentiable function are not
differentiable.
10.38
Example.
If
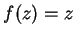
for all
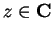
, then

is differentiable and
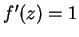
. However,
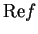
is nowhere differentiable. In fact, if
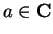
,
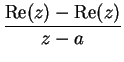
has no limit at

. To see this, let
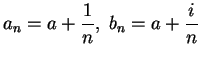
for all
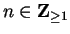
. Then
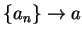
,
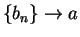
, and
and
Hence, the sequences
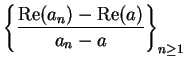
and
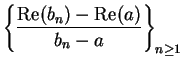
have
different limits, so
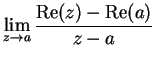
does not
exist.
However, we do have the following theorem.
10.39
Theorem.
Let 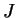 be an interval in
be an interval in
 and let
and let
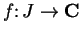 be a function
differentiable at a point
be a function
differentiable at a point 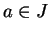 . Write
. Write
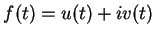 where
where 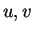 are real
valued. Then
are real
valued. Then 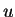 and
and 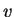 are differentiable at
are differentiable at  , and
, and
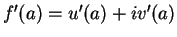 .
.
Proof: Since  is differentiable at
is differentiable at  there is a function
there is a function
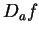 on
on 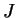 such that
such that 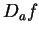 is continuous at
is continuous at  and
and
If
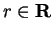 and
and
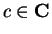 , then
, then
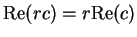 and
and
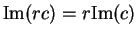 , so
, so
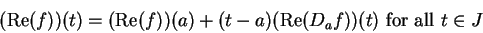 |
(10.40) |
and
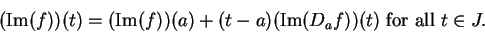 |
(10.41) |
Since 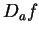 is continuous at
is continuous at  ,
,
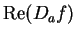 and
and
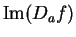 are
continuous at
are
continuous at  , so equations (10.40) and (10.41) show that
, so equations (10.40) and (10.41) show that
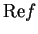 and
and
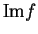 are differentiable and
are differentiable and
10.42
Example.
Let
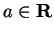
, and let
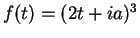
for all
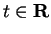
.
Then

is differentiable and (by
the chain rule),
We have by direct calculation,
so
(This example just illustrates that the theorem is true in a special case.)
10.43
Theorem.
Let  be a complex function and let
be a complex function and let
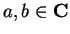 , and suppose
, and suppose
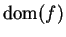 contains the
line segment
contains the
line segment 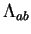 , and that
, and that 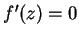 for all
for all
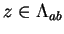 . Then
. Then
 is constant on
is constant on 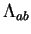 ; i.e.,
; i.e., 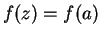 for all
for all
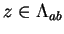 .
.
Proof: Define a function
![$F\colon[0,1]\to\mbox{{\bf C}}$](img1238.gif) by
by
By the chain rule, 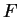 is differentiable on
is differentiable on ![$[0,1]$](img1240.gif) and
and
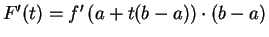 . Since
. Since 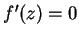 for all
for all
![$z\in\Lambda_{ab}([0,1])$](img1242.gif) , we have
, we have 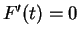 for all
for all ![$t\in[0,1]$](img1244.gif) . Hence
. Hence
and hence
If
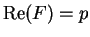 and
and
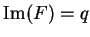 , then
, then 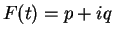 for all
for all ![$t\in[0,1]$](img1244.gif) .
.





Next: 10.3 Trigonometric Functions
Up: 10. The Derivative
Previous: 10.1 Derivatives of Complex
Index
![]() has a maximum at
has a maximum at ![]() ,
,
![]() ,
, ![]() in
in
![]() by
by
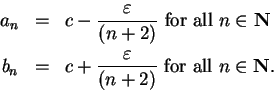
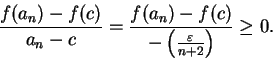
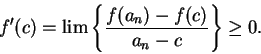
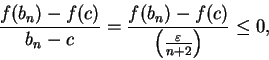
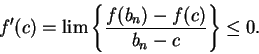
![]() has a maximum at some point
has a maximum at some point
![]() . If
. If ![]() , then the critical point theorem says
, then the critical point theorem says ![]() , and we
are finished. Suppose
, and we
are finished. Suppose ![]() . We know there is a point
. We know there is a point ![]() such
that
such
that ![]() has a minimum at
has a minimum at ![]() . If
. If ![]() we get
we get ![]() by the critical
point theorem, so suppose
by the critical
point theorem, so suppose ![]() . Then since
. Then since ![]() and
and
![]() , we have
, we have ![]() , and it follows that
, and it follows that ![]() is a
constant function on
is a
constant function on ![]() , and in this case
, and in this case ![]() for all
for all ![]() .
.
![]()
![]() at some point
at some point
![]() is parallel to the chord joining
is parallel to the chord joining
![]() to
to
![]() .
.
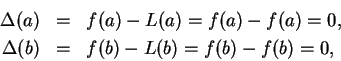
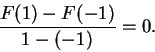
![\begin{eqnarray*}
\mbox{\rm int}( [a,b)) = \mbox{\rm int}([a,b]) = \mbox{\rm int...
...rm int}([a,\infty)) = \mbox{\rm int}((a,\infty)) &=& (a,\infty).
\end{eqnarray*}](img1150.gif)
![]() is an interval, and
is an interval, and ![]() are points in
are points in ![]() with
with
![]() , then every point in
, then every point in ![]() is in the interior of
is in the interior of ![]() .
.
![]() for all
for all
![]() . Then for all
. Then for all ![]() with
with ![]() we have
we have ![]() is continuous on
is continuous on ![]() and differentiable
on
and differentiable
on ![]() , so by the mean value theorem
, so by the mean value theorem
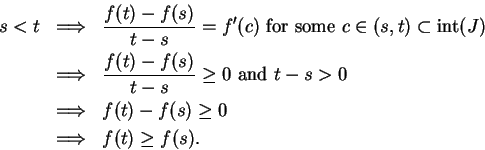
![]() is differentiable on
is differentiable on ![]() and
and ![]() is strictly increasing
on
is strictly increasing
on ![]() , then
, then ![]() for all
for all ![]() .
.
![]() is differentiable on
is differentiable on ![]() , and
, and ![]() has a maximum at
has a maximum at
![]() ,
then
,
then ![]() .
.
![]() is continuous on
is continuous on ![]() and
and ![]() is differentiable on
is differentiable on
![]() , and
, and ![]() for all
for all ![]() , then
, then ![]() is strictly
increasing on
is strictly
increasing on ![]() .
.
![]() be a subset of
be a subset of
![]() , let
, let
![]() , and let
, and let ![]() be a point such that
be a point such that ![]() is differentiable at
is differentiable at ![]() . Let
. Let ![]() be a subset
of
be a subset
of ![]() containing
containing ![]() , and let
, and let
![]() be the restriction of
be the restriction of
![]() to
to ![]() , i.e.
, i.e.
![]() be any sequence in
be any sequence in
![]() such that
such that
![]() . Then
. Then ![]() is a sequence in
is a sequence in
![]() ,
and hence
,
and hence
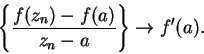
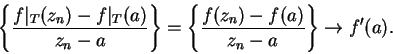
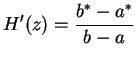 for all
for all
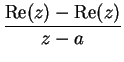 has no limit at
has no limit at 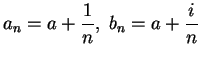 for all
for all
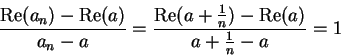
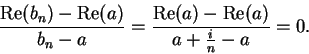
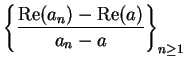 and
and
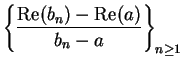 have
different limits, so
have
different limits, so
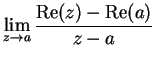 does not
exist.
does not
exist.
![]() is differentiable at
is differentiable at ![]() there is a function
there is a function
![]() on
on ![]() such that
such that ![]() is continuous at
is continuous at ![]() and
and
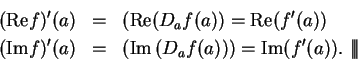
![\begin{eqnarray*}
f'(t)&=&3(2t+ia)^2\cdot 2\\
&=&6[(4t^2-a^2)+4iat] \\
&=&(24t^2-6a^2)+24iat.
\end{eqnarray*}](img1233.gif)
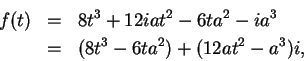
![]() by
by