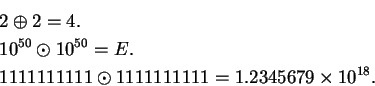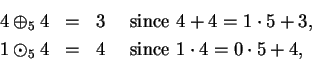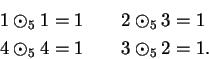Next: 2.3 The Field Axioms
Up: 2. Fields
Previous: 2.1 Binary Operations
Index
2.2 Some Examples
2.35
Example (Calculator operations.)
Let
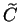
denote the set of all numbers that can be entered into your
calculator. The exact composition of
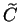
depends on the model of your
calculator. Let
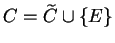
where
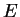
is some object not in
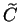
. I
will call
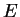 the error
the error. I think of
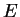
as the result produced when you enter
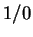
. Define four binary operations
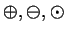
, and
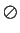
on
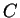
by
On my calculator
If

denotes any of
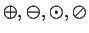
, I define
On all calculators with which I am familiar,
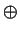
and
are commutative operations,

is an
identity for
,
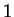
is an identity for
, and every element of
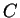
except for
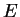
is invertible for
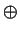
. On my calculator
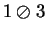 |
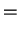 |
 |
(2.36) |
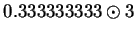 |
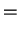 |
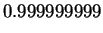 |
(2.37) |
 |
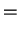 |
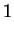 |
(2.38) |
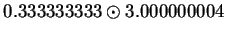 |
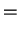 |
 |
(2.39) |
Thus
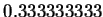
has two different inverses! It follows from theorem
2.15 that
is not associative. Your calculator may give different
results for the calculations (
2.38) and (
2.39) but none of the
calculator operations are associative.
2.40
Exercise.
A
Verify that calculator addition
and calculator
multiplication

are not associative, by finding calculator numbers

,
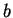
,
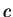
,

,
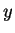
, and
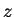
such that

, and
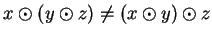
.
2.41
Notation.
If

, let
Hence, for example
2.42
Definition (
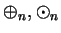 .)
.)
Let

, with
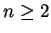
. We define two binary operations
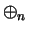
and
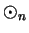
on
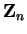
by:
for all
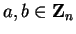 ,
,
and for all
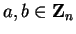 ,
,
Thus,
and
The operations 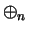 and
and 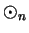 are both commutative (since
are both commutative (since  and
and  are commutative on
are commutative on
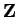 ). Clearly
). Clearly  is an identity for
is an identity for 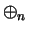 , and
, and 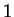 is an
identity for
is an
identity for 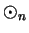 . Every element of
. Every element of
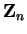 is invertible for
is invertible for 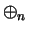 and
and
2.43
Definition (Multiplication table.)
Let

be a binary operation on a finite set
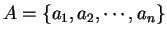
having

elements. We construct a
multiplication table for

as follows: We
write down a table with

rows and

columns. Along the top of the table we list
the elements of

as labels for the columns. Along the left side of the table we
list the elements of

(in the same order) as labels for the rows. (See the figure
to see what is meant by this.) If
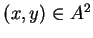
, we write the product
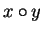
in
the box of our table whose row label is

and whose column label is
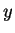
.
Multiplication table for

2.44
Examples.
Below are the multiplication tables for
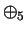
and
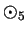
:
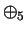 |
0 |
1 |
2 |
3 |
4 |
| 0 |
0 |
1 |
2 |
3 |
4 |
| 1 |
1 |
2 |
3 |
4 |
0 |
| 2 |
2 |
3 |
4 |
0 |
1 |
| 3 |
3 |
4 |
0 |
1 |
2 |
| 4 |
4 |
0 |
1 |
2 |
3 |
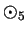 |
0 |
1 |
2 |
3 |
4 |
| 0 |
0 |
0 |
0 |
0 |
0 |
| 1 |
0 |
1 |
2 |
3 |
4 |
| 2 |
0 |
2 |
4 |
1 |
3 |
| 3 |
0 |
3 |
1 |
4 |
2 |
| 4 |
0 |
4 |
3 |
2 |
1 |
By looking at the multiplication table for 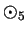 we see that
we see that
Hence all the non-zero elements of
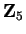 have inverses under
have inverses under 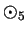 .
.
Both of the operations 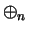 and
and 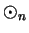 are associative. This follows from
the fact that
are associative. This follows from
the fact that 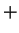 and
and 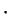 are associative operations on
are associative operations on
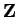 , by a
straightforward but lengthy argument. The details are given in appendix
B.
, by a
straightforward but lengthy argument. The details are given in appendix
B.
2.45
Exercise.
Write down the multiplication table for
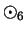
on
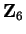
. Determine which
elements of
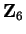
are invertible for
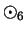
, and find the inverse for each
invertible element.
2.46
Exercise.
Let
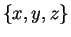
be a set containing three distinct elements.

,
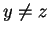
,
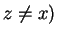
.
Let

be the binary operation on
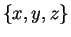
determined by the
multiplication table:
- a)
- Show that there is an identity element for
 . (Which of
. (Which of 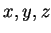 is the
identity?)
is the
identity?)
- b)
- Show that
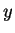 has two different inverses for
has two different inverses for  .
.
- c)
- Explain why the result of part b does not contradict the theorem on uniqueness
of inverses.
2.47
Note.
An early example of a binary operation that was not an obvious
generalization of one of the operations
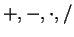
on numbers was the use of union
and intersection as binary operations on the set of all sets by George
Boole[
11]. In
Laws of Thought (1854),
Boole introduces the operation
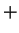
(for union) and
(for intersection) on `` classes" (although he
usually writes
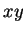
instead of
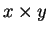
). He explicitly states
which he calls commutative and distributive laws. He does not mention associativity,
and writes
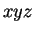
without parentheses. He denotes `` Nothing" by

and ``
the Universe" by
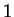
, and notes that

and
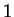
have the usual properties. As an
example of the distributive law, Boole gives
European men and women
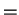
European men
and European women.
Boole's 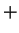 is not really a binary operation since he only
defines
is not really a binary operation since he only
defines 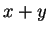 when
when  and
and 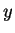 have no elements in common.
have no elements in common.
The word associative, in its mathematical sense, was introduced by
William Hamilton[24, p114] in
1843
in a paper on quaternions. According to
[14, p284], the words commutative and distributive were
introduced by Francois -Joseph Servois in 1813.




Next: 2.3 The Field Axioms
Up: 2. Fields
Previous: 2.1 Binary Operations
Index

![]()
![]()
![]() , Maple first found that
, Maple first found that ![]() is false, and then,
without looking at
is false, and then,
without looking at ![]() , concluded that
, concluded that ![]()
![]()
![]() must be false.
When evaluating
must be false.
When evaluating ![]()
![]()
![]() , Maple first tried to evaluate
, Maple first tried to evaluate ![]() , and
in the process discovered that
, and
in the process discovered that ![]() is not a proposition. Mathematically,
both
is not a proposition. Mathematically,
both ![]()
![]()
![]() and
and ![]()
![]()
![]() are errors when
are errors when ![]() and
and ![]() .
Many programmers consider the non-commutativity of
.
Many programmers consider the non-commutativity of ![]() to be a
feature (i.e. good), rather than
a bug (i.e. bad).
to be a
feature (i.e. good), rather than
a bug (i.e. bad).