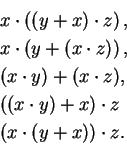Next: 2.4 Some Consequences of
Up: 2. Fields
Previous: 2.2 Some Examples
Index
We often speak of `` the field  " instead of ``
the field
" instead of ``
the field  ".
".
2.49
Remark.
Most calculus books that begin with the axioms for a field (e.g.,
[
47, p5], [
1, p18], [
13, p5], [
12, p554])
add an additional axiom.
- 10.
- (Commutativity of addition.) Addition is a commutative operation on
 .
.
I have omitted this because, as Leonard Dickson
pointed out in 1905[
18, p202], it
can be proved from the other axioms (see theorem
2.72 for a proof). I
agree with Aristotle that
It is manifest that it is far better to make the principles finite in
number. Nay, they should be the fewest possible provided they enable all the same
results to be proved. This is what mathematicians insist upon; for they take as
principles things finite either in kind or in number[26, p178].
2.50
Remark (Parentheses.)
The distributive law is usually written as
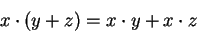 |
(2.51) |
The right side of (
2.51) is ambiguous. There are five sensible ways to
interpret it:
The conventions presently used for interpreting ambiguous statements such as
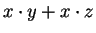
and involving operations
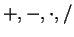
are:
- Multiplication and division have equal precedence.
- Addition and subtraction have equal precedence.
- Multiplication has higher precedence than addition.
This means that to interpret
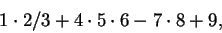 |
(2.52) |
you first read (
2.52) from left to right and perform all the multipliations and
divisions as you come to them, getting
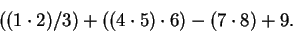 |
(2.53) |
Then read (
2.53) from left to right performing all additions and subtractions
as you come to them, getting
When I was in high school, multiplication had higher precedence than division, so
meant
whereas today it means
In 1713, addition often had higher precedence than multiplication.
Jacob Bernoulli
[
8, p180] wrote expressions like
to mean
2.56
Exercise.
Determine for which values of
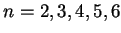
,
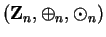
is a
field. (You already know that
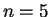
produces a field.)
2.57
Notation (The field
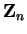 .)
.)
Let

,
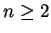
be a number such that
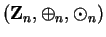
is a field.
Then `` the field
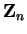
" means the field
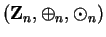
. I will
often denote the operations in
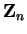
by
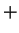
and
instead of
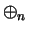
and
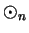
.
2.58
Entertainment.
Determine for which values of

in
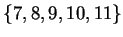
the system
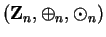
is a field. If you do this you will probably conjecture
the exact (fairly simple) condition on

that makes the system into a field.




Next: 2.4 Some Consequences of
Up: 2. Fields
Previous: 2.2 Some Examples
Index
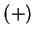 is an associative operation
on
is an associative operation
on  .
.
 .
.
 of
of  is invertible
for
is invertible
for 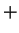 .
.
 is unique, and we will denote it
by
is unique, and we will denote it
by 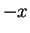 .
.
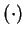 is a
commutative operation on
is a
commutative operation on  .
.
 .
.
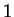 .
.
 of
of  except possibly for
except possibly for  is invertible for
is invertible for 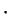 .
.
 is unique, and we will denote it by
is unique, and we will denote it by 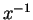 .
We do not
assume
.
We do not
assume  is not invertible. We just do not assume that it is.
is not invertible. We just do not assume that it is.
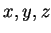 in
in  ,
,
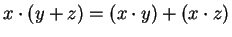 .
.
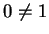 .
.