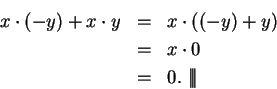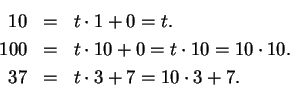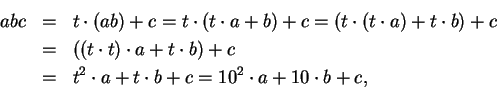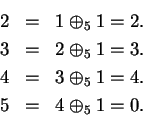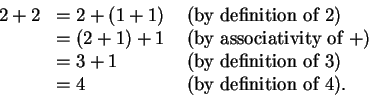Next: 2.5 Subtraction and Division
Up: 2. Fields
Previous: 2.3 The Field Axioms
Index
Proof: All of these results are special cases of the cancellation law for an
associative operation (theorem 2.19).

2.64
Theorem.
In any field 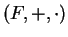
Proof: These are special cases of the remark made earlier that an identity
element is always invertible, and is its own inverse.

2.65
Theorem (Double inverse theorem.)
In any field 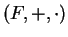 ,
,
Proof: These are special cases of theorem 2.17.

I will now start the practice of calling a field  . If I say `` let
. If I say `` let  be a
field" I assume that the operations are denoted by
be a
field" I assume that the operations are denoted by 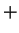 and
and 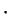 .
.
2.66
Theorem.
Let

be a field. Then
Proof: We know that 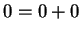 , and hence
, and hence
Also,
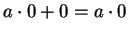 , so
, so
By the cancellation law for addition, 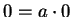 .
.

2.67
Corollary.
Let  be a field. Then for all
be a field. Then for all 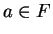 ,
, 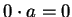 .
.
Proof:
- Case 1:
- Suppose
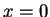 . Then (2.69) is true because every statement implies a
true statement.
. Then (2.69) is true because every statement implies a
true statement.
- Case 2:
- Suppose
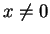 . By theorem 2.66,
. By theorem 2.66, 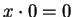 , so
, so
Since 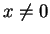 , we can use the cancellation law for multiplication to get
, we can use the cancellation law for multiplication to get
and hence
Thus (2.69) holds in all cases.

2.70
Remark.
We can combine theorem
2.66, corollary
2.67 and theorem
2.68 into the statement: In any field

,
2.71
Exercise.
Let

be a field. Prove that

has no multiplicative inverse in

.
2.72
Theorem (Commutativity of addition.)
Let  be any field. Then
be any field. Then 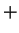 is a commutative operation on
is a commutative operation on  .
.
Proof: Let 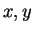 be elements in
be elements in  . Then since multiplication is
commutative, we have
. Then since multiplication is
commutative, we have
By the distributive law,
Since 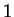 is the multiplicative identity,
is the multiplicative identity,
and hence
By the cancellation law for addition
By commutativity of multiplication and the distributive law,
and
Since 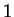 is the multiplicative identity and addition is associative
is the multiplicative identity and addition is associative
and hence
Since multiplication is commutative
and by the cancellation law for addition,
Hence, 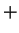 is commutative.
is commutative.

2.73
Remark.
Let

be a field, and let
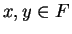
. Then
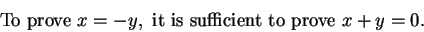 |
(2.74) |
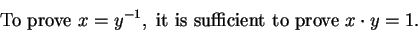 |
(2.75) |
Proof:
2.76
Theorem.
Let  be a field. Then
be a field. Then
Proof: Let 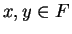 . By (2.74) it is sufficient to prove
. By (2.74) it is sufficient to prove
Well,
2.78
Exercise.
A
Let

be a field and let
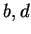
be non-zero elements in

. Prove that
2.79
Definition (Digits.)
Let

be a field. We define
I'll call the set
the set of
digits in 
.
If
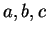
are digits, I define
 |
(2.80) |
and
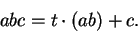 |
(2.81) |
Here
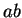
should not be confused with
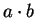
.
2.82
Example.
In general, if
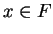
, I define
Then for all digits
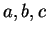
so, for example
2.83
Remark.
The set
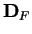
of digits in

may contain fewer than ten elements. For
example, in
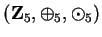
,
and you can see that
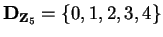
.
2.84
Theorem.
In any field  ,
, 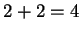 and
and 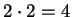 .
.
Proof:
Also,
2.85
Exercise.
Prove that in any field

,
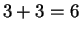
and

.
2.86
Exercise.
Prove that in any field

,
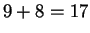
.
2.87
Remark.
After doing the previous two exercises, you should believe that the
multiplication and addition tables that you learned in elementary school are all
theorems that hold in any field, and you should feel free to use them in any
field.
2.88
Exercise.
Let

be a field and let
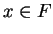
. Prove that




Next: 2.5 Subtraction and Division
Up: 2. Fields
Previous: 2.3 The Field Axioms
Index
![]()
![]()
![]()
![]() . If I say `` let
. If I say `` let ![]() be a
field" I assume that the operations are denoted by
be a
field" I assume that the operations are denoted by ![]() and
and ![]() .
.
![]() , and hence
, and hence
![]() be elements in
be elements in ![]() . Then since multiplication is
commutative, we have
. Then since multiplication is
commutative, we have
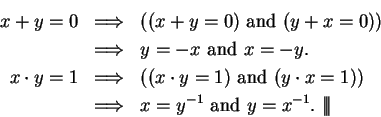
![]() . By (2.74) it is sufficient to prove
. By (2.74) it is sufficient to prove