



Next: 2.6 Ordered Fields
Up: 2. Fields
Previous: 2.4 Some Consequences of
Index
2.5 Subtraction and Division
2.89
Definition (Subtraction.)
In any field

, we define a binary operation
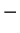
(called subtraction) by
Unfortunately we are now using the same symbol
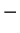
for two different things, a binary
operation on

, and a symbol denoting additive inverses.
2.90
Exercise (Distributive laws.)
A
Let

be a field, and let
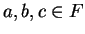
. Prove that
- [a)]
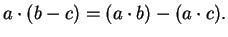
- [b)]
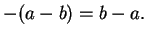
2.91
Definition (Division.)
Let

be a field. If
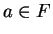
and
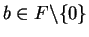
we define
We also write
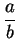
for
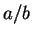
. If
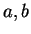
are both in
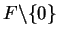
,
then
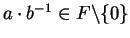
so
defines a binary operation on
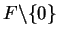
. Also, if
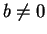
, then
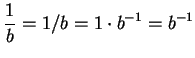
.
2.92
Example.
In the field
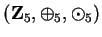
,
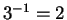
and
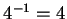
. Hence
Thus,
I will now start the practice of using steps in proofs that involve multiple uses of
the associative and commutative laws. For example, I'll write statements such as
with no explanation, because I believe that you recognize that it is correct, and
that you can prove it. I'll also write 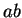 for
for 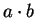 when I believe that no
confusion will result, and I'll use distributive laws like
when I believe that no
confusion will result, and I'll use distributive laws like
and
even though we haven't proved them. I will write
and assume that you know (because of our conventions about omitting parentheses; cf.
Remark 2.50) that the right side of this means
and you also know (by exercise 2.30) that the parentheses can be rearranged
in other sensible orders without changing the value of the expression.
2.95
Theorem.
Let  be a field. Then for all
be a field. Then for all 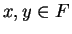 ,
,
Proof:
Proof: The proof uses the algebraic identity
Since 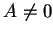 and
and 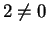 , we have
, we have 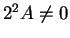 and hence
and hence
Hence if 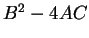 is not a square, then (2.97) has no solutions. If
is not a square, then (2.97) has no solutions. If
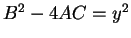 for some
for some 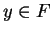 , then
, then
2.99
Note.
The definition of field that we use is roughly equivalent to the definition given by
H. Weber in 1893
[
48, p526]. Weber does not give the zero-one axiom
but he remarks that

is different from
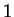
except in the uninteresting case where
the field has only one element. He includes commutativity of addition as an axiom,
and he also appears to take
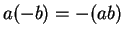
as an axiom. Individual fields, both
finite fields and subfields of the real and complex numbers, had been studied before
Weber's paper, but Weber's definition provided an abstraction that included both
finite and infinite fields.
There are many other choices we could have made for the field axioms. In
[29], Edward Huntington
gives eight different sets of axioms that are
equivalent to ours. (Two sets of propositions
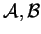 are equivalent if every statement in
are equivalent if every statement in 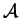 can be proved using
statements in
can be proved using
statements in 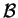 , and every statement in
, and every statement in 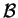 can
be proved from statements in
can
be proved from statements in 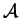 .)
.)




Next: 2.6 Ordered Fields
Up: 2. Fields
Previous: 2.4 Some Consequences of
Index
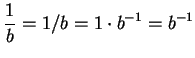 .
.
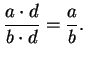
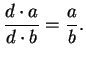
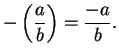
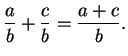
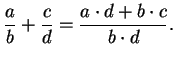
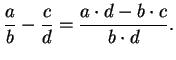
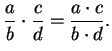
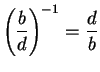 .
.
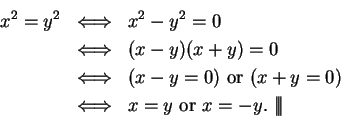
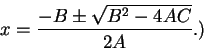
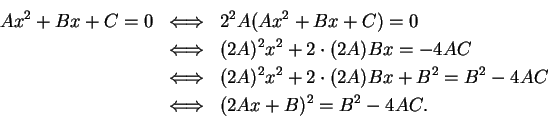
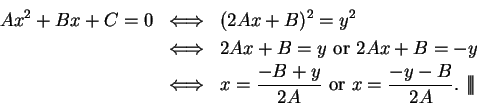
![]() are equivalent if every statement in
are equivalent if every statement in ![]() can be proved using
statements in
can be proved using
statements in ![]() , and every statement in
, and every statement in ![]() can
be proved from statements in
can
be proved from statements in ![]() .)
.)