



Next: 6.5 Complex Functions
Up: 6. The Complex Numbers
Previous: 6.3 Roots of Complex
Index
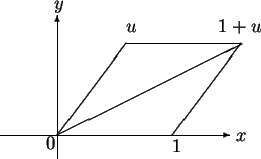
Let 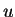 be a direction in
be a direction in 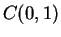 , with
, with 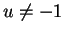 . Then we know that
. Then we know that 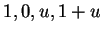 are
the vertices of a parallelogram.
are
the vertices of a parallelogram.
Since 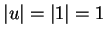 , all four sides of the
parallelogram are equal, and thus the parallelogram is a rhombus. Since the
diagonals of a rhombus bisect its angles, the segment from
, all four sides of the
parallelogram are equal, and thus the parallelogram is a rhombus. Since the
diagonals of a rhombus bisect its angles, the segment from  to
to 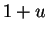 bisects angle
bisects angle
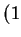 -
- -
-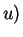 . Hence I expect that the direction of
. Hence I expect that the direction of 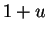 (i.e.,
(i.e.,
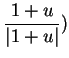 is a square root of
is a square root of 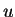 . I can prove that this is the case without using any
geometry.
. I can prove that this is the case without using any
geometry.
6.23
Theorem.
Let 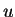 be a direction in
be a direction in
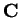 with
with 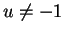 . Then
. Then
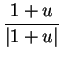 is
a square root of
is
a square root of 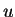 .
.
Proof: I just need to square
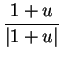 . Well,
. Well,
Now since 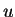 is a direction, we know that
is a direction, we know that 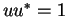 , and hence
, and hence
6.24
Corollary.
Every complex number has a square root.
Proof: Let
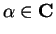 . If
. If 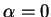 , then clearly
, then clearly 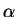 has a square root.
If
has a square root.
If 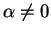 , let
, let 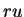 be the polar decomposition for
be the polar decomposition for 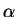 . If
. If 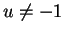 ,
then
,
then
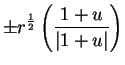 are square roots of
are square roots of 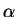 .
If
.
If 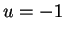 , then
, then
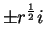 are square roots of
are square roots of 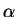 .
.

6.25
Example.
We will find the square roots of
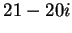
.
Let
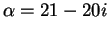
. Then
Hence the polar decomposition for
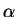
is
The square roots of
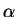
are
Now
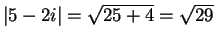
, so the square roots of
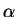
are
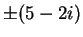
.
6.26
Exercise.
Find the square roots of
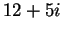
. Write your
answers in the form
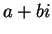
, where

and
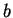
are real.
A
Let
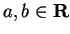 . There is a formula for the square root of
. There is a formula for the square root of 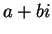 that allows you to
say
that allows you to
say
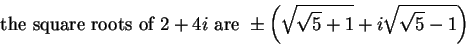 |
(6.27) |
and
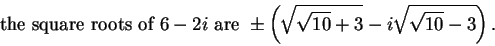 |
(6.28) |
6.29
Exercise.
Verify that assertions (
6.27) and (
6.28) are correct.




Next: 6.5 Complex Functions
Up: 6. The Complex Numbers
Previous: 6.3 Roots of Complex
Index

![]() , all four sides of the
parallelogram are equal, and thus the parallelogram is a rhombus. Since the
diagonals of a rhombus bisect its angles, the segment from
, all four sides of the
parallelogram are equal, and thus the parallelogram is a rhombus. Since the
diagonals of a rhombus bisect its angles, the segment from ![]() to
to ![]() bisects angle
bisects angle
![]() -
-![]() -
-![]() . Hence I expect that the direction of
. Hence I expect that the direction of ![]() (i.e.,
(i.e.,
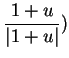 is a square root of
is a square root of ![]() . I can prove that this is the case without using any
geometry.
. I can prove that this is the case without using any
geometry.
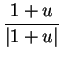 . Well,
. Well,
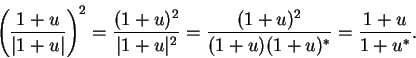
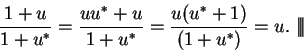
![]() . If
. If ![]() , then clearly
, then clearly ![]() has a square root.
If
has a square root.
If ![]() , let
, let ![]() be the polar decomposition for
be the polar decomposition for ![]() . If
. If ![]() ,
then
,
then
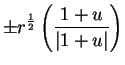 are square roots of
are square roots of ![]() .
If
.
If ![]() , then
, then
![]() are square roots of
are square roots of ![]() .
.
![]()
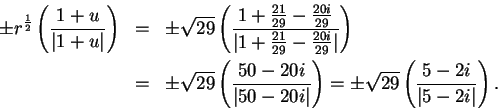
![]() . There is a formula for the square root of
. There is a formula for the square root of ![]() that allows you to
say
that allows you to
say