



Next: 7. Complex Sequences
Up: 6. The Complex Numbers
Previous: 6.4 Square Roots
Index
When one studies a function  from
from
 to
to
 , one often gets information by
looking at the graph of
, one often gets information by
looking at the graph of  , which is a subset of
, which is a subset of
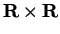 . If we consider a
function
. If we consider a
function
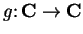 , the graph of
, the graph of 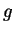 is a subset of
is a subset of
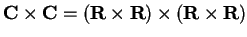 , and
, and
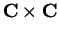 is a ``
4-dimensional" object which cannot be visualized. We will now discuss a method to
represent functions from
is a ``
4-dimensional" object which cannot be visualized. We will now discuss a method to
represent functions from
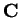 to
to
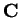 geometrically.
geometrically.
6.31
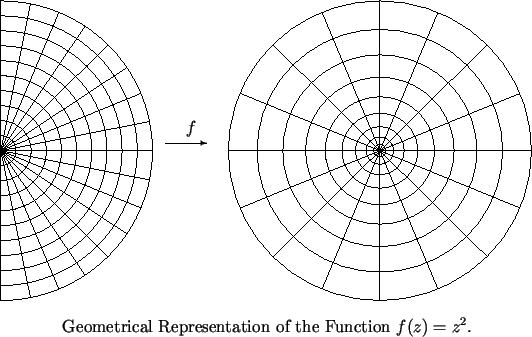
Example (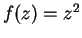 .)
.)
Let
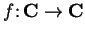
be defined by
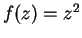
. If
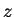
is a point in the circle
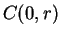
, then
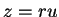
where
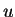
is a direction, and
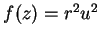
is a point in the
circle
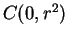
with radius
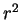
.
Thus

maps circles of radius
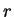
about

into circles of radius
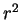
about

. Let
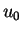
be a direction in
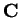
. If
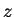
is
on the ray from

passing through
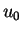
, then
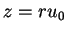
for some
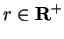
so
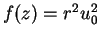
, which is on the ray from

passing through
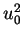
. Hence the ray
making an angle
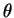
with the positive real axis gets mapped by

to the ray
making an angle
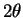
with the positive

-axis.
The left part of the figure shows a network formed by semicircles of radius
and rays making angles
with the positive

-axis. The right part of the figure shows the network formed by
circles of radius
and rays making angles
with the positive

-axis.

maps each semicircle in the left part of the figure
to a circle in the right part, and

maps each ray in the left part to a ray in the
right part. Also

maps each curvilinear rectangle on the left to a curvilinear
rectangle on the right. Notice that
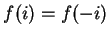
, and in general
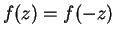
, so if
we know how

maps points in the right half plane, we know how it maps points in
the left half plane. The function

maps the right half plane
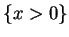
onto
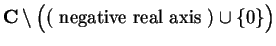
.
6.32
Definition (Image of a function.)
Let
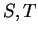
be sets, let
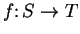
, and let

be a subset of
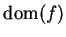
.
We
define
and we call
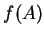
the
image of  under
under 
. We call
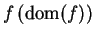
the
image of 
.
6.33
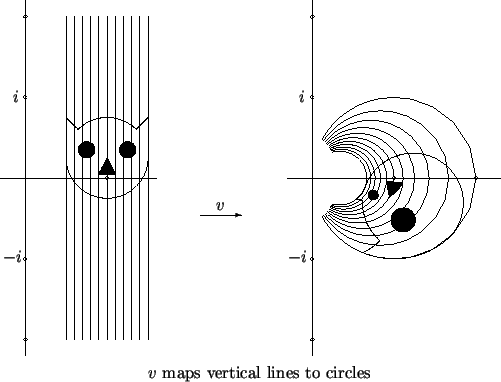
Example (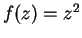 , continued)
, continued)
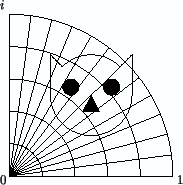
In the figure above
6.5, the right half of the figure
is the image of the left half under the function

.
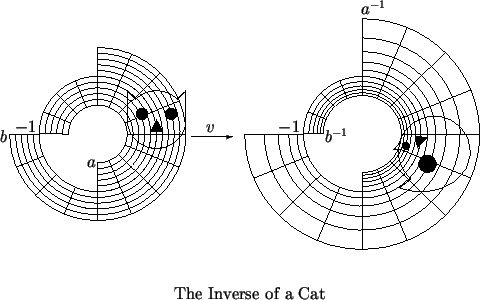
The figure below
6.5, shows the image of a
cat-shaped set under

. The cat on
the left lies in the first quadrant, so its square lies in the first two quadrants.
The tip of the right ear is
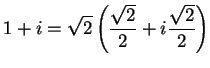
, with length
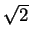
, and with direction making an angle
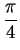
with the positive real axis. The image of the right ear has length
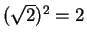
and makes an angle
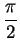
with the positive

-axis. You
should examine how the parts of the cat in each curvilinear rectangle on the left
part of the figure correspond to their images on the right part.
6.34
Exercise.
Let
be the cat shown in the left part of the above figure. Sketch the
image of
under each of the functions
below:
- a)
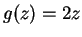 .
.
- b)
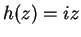 .
.
- c)
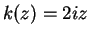 .
.
6.35
Exercise.
Let
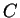
be the cat shown in the left part of the above figure. Sketch the
image of
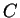
under
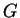
, where
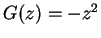
.
6.36
Exercise.
Let
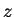
be a direction in
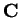
; i.e., let
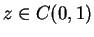
. Show that
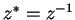
.
6.37
Example.
Let
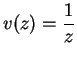
for all
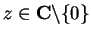
. If
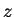
is in the circle
of radius
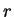
, then
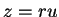
for some direction
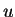
, and
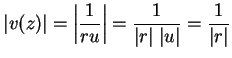
, so
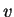
takes points in the
circle of radius
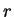
about

to points in the circle of radius
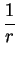
about

.
Let 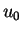 be a direction. If
be a direction. If 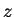 is in the ray from
is in the ray from  through
through 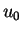 , then
, then 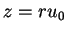 for some
for some
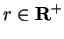 , so
, so
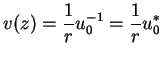 . We noted
earlier that
. We noted
earlier that 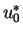 is the reflection of
is the reflection of 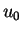 about the real axis, so
about the real axis, so 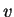 maps the
ray making angle
maps the
ray making angle 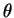 with the positive real axis into the ray making angle
with the positive real axis into the ray making angle
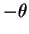 with the positive real axis.
Thus
with the positive real axis.
Thus 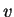 maps the network of circles and lines in the left half of the figure
into the network on the right half.
maps the network of circles and lines in the left half of the figure
into the network on the right half.
The circular arcs in the left half of the figure have radii
Let's see how 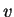 maps the vertical line
maps the vertical line
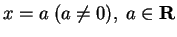 . We know that
. We know that
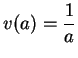 and
and 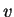 maps points in the upper half plane to points in the
lower half plane. Points far from the origin get mapped to points near to the
origin. I claim that
maps points in the upper half plane to points in the
lower half plane. Points far from the origin get mapped to points near to the
origin. I claim that 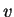 maps the line
maps the line 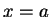 into the circle with center
into the circle with center
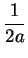 and radius
and radius
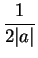 .
.
Let
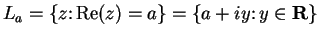 , so
, so 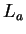 is the set of points
in the line
is the set of points
in the line 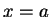 . Then
. Then
since
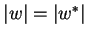
for all
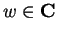
. Hence,
and
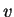
maps every point in
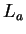
into
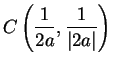
. Now I claim that every point in
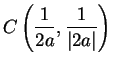
(except for

) is equal to
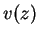
for some
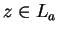
.
Since
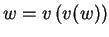 , it will be sufficient to show that if
, it will be sufficient to show that if
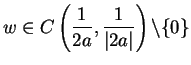 , then
, then 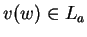 . I want to
show
. I want to
show
Well, suppose
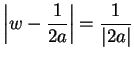
,
and let
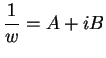
where
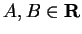
. Then
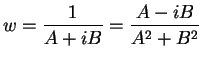
, so
so (by definition of

)
6.38
Exercise.
The argument above does not apply to the vertical line
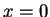
. Let
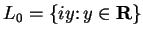
. Where does the reciprocal function
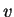
map
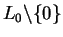
?
6.39
Entertainment.
Let
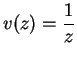
for all
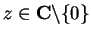
. Show that
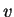
maps
horizontal lines
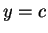
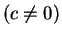
into circles that pass through the origin. Sketch
the images of the lines
and the lines
on one set of axes using a compass. If you've done this correctly,
the circles
should intersect at right angles.
6.40
Exercise.
- a)
- Sketch the image of the network of lines and circular arcs shown below under
the function
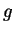 , where
, where 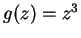 for all
for all
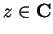 .
.
- b)
- Cube the cat in the picture.
6.41
Note.
De Moivre's formula
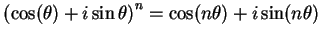
, was first
stated in this form by Euler
in 1749 ([
46, pp. 452-454]). Euler named the
formula after Abraham De Moivre (1667-1754) who never explicitly stated the formula,
but used its consequences several times ([
46, pp. 440-450]).
The method for finding 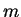 th roots of complex numbers:
th roots of complex numbers:
was introduced by Euler in 1749 [
46, pp.452-454].
The idea of illustrating functions from the plane to the plane by distorting cat
faces is due to Vladimir Arnold (1937-??), and the figures are sometimes called ``
Arnold Cats". Usually Arnold cats have black faces and white eyes and noses, as in
[3, pp.6-9].




Next: 7. Complex Sequences
Up: 6. The Complex Numbers
Previous: 6.4 Square Roots
Index


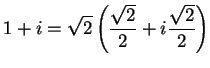 , with length
, with length 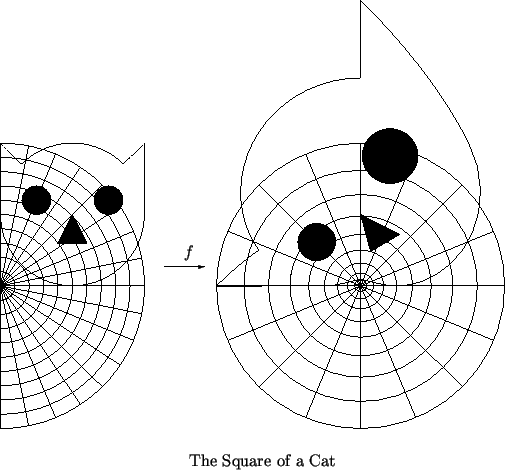
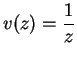 for all
for all
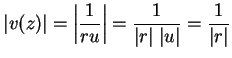 , so
, so ![]() be a direction. If
be a direction. If ![]() is in the ray from
is in the ray from ![]() through
through ![]() , then
, then ![]() for some
for some
![]() , so
, so
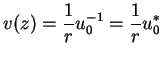 . We noted
earlier that
. We noted
earlier that ![]() is the reflection of
is the reflection of ![]() about the real axis, so
about the real axis, so ![]() maps the
ray making angle
maps the
ray making angle ![]() with the positive real axis into the ray making angle
with the positive real axis into the ray making angle
![]() with the positive real axis.
Thus
with the positive real axis.
Thus ![]() maps the network of circles and lines in the left half of the figure
into the network on the right half.
maps the network of circles and lines in the left half of the figure
into the network on the right half.
![]() maps the vertical line
maps the vertical line
![]() . We know that
. We know that
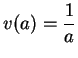 and
and ![]() maps points in the upper half plane to points in the
lower half plane. Points far from the origin get mapped to points near to the
origin. I claim that
maps points in the upper half plane to points in the
lower half plane. Points far from the origin get mapped to points near to the
origin. I claim that ![]() maps the line
maps the line ![]() into the circle with center
into the circle with center
![]() and radius
and radius
![]() .
.
![]() , so
, so ![]() is the set of points
in the line
is the set of points
in the line ![]() . Then
. Then
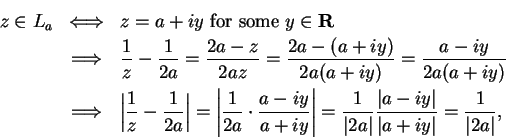
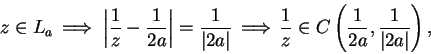
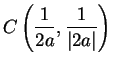 . Now I claim that every point in
. Now I claim that every point in
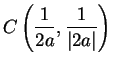 (except for
(except for ![]() , it will be sufficient to show that if
, it will be sufficient to show that if
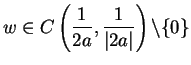 , then
, then ![]() . I want to
show
. I want to
show
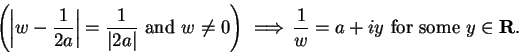
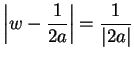 ,
and let
,
and let
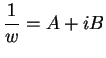 where
where
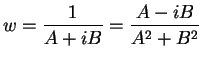 , so
, so
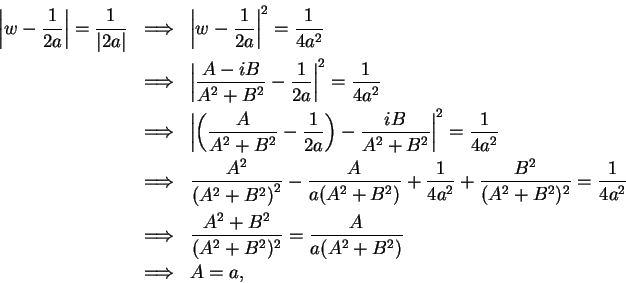
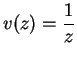 for all
for all
![]() th roots of complex numbers:
th roots of complex numbers:
![\begin{displaymath}[r(\cos\theta+i\sin\theta)]^{{1\over m}}=r^{{1\over m}}\left[\cos{\theta\over
m}+i\sin{\theta\over m}\right]\end{displaymath}](img1765.gif)