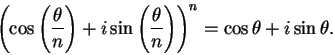
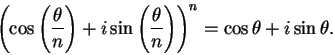
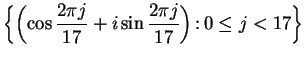 .
.

Let
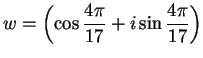 and
and
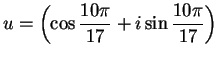 . Draw the
polygons
. Draw the
polygons ![]() -
-![]() -
-![]() -
-![]() -
-![]() and
and ![]() -
-![]() -
-![]() -
-![]() -
-![]() on different sets of axes, (i.e. draw segments connecting
on different sets of axes, (i.e. draw segments connecting ![]() to
to ![]() ,
, ![]() to
to ![]() ,
,
![]() ,
, ![]() to
to ![]() , and segnents joining
, and segnents joining ![]() to
to ![]() ,
, ![]() ,
, ![]() to
to ![]() .)
.)
Proof: If ![]() where
where
![]() and
and ![]() , then we have
, then we have
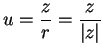 .
Since
.
Since
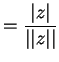
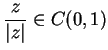 and
and
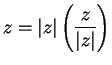 gives
the desired decomposition.
gives
the desired decomposition.