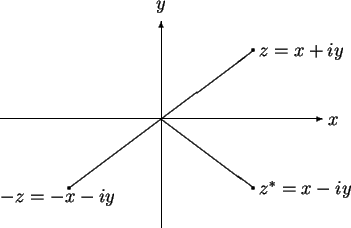

Then
![]() is identified with the
is identified with the ![]() -axis, and points on the
-axis, and points on the ![]() -axis are of the
form
-axis are of the
form ![]() where
where ![]() is real. I will call the
is real. I will call the ![]() -axis the real axis,
and I'll
call the
-axis the real axis,
and I'll
call the ![]() -axis the imaginary axis.
If
-axis the imaginary axis.
If
![]() , then
, then ![]() represents the
result of reflecting
represents the
result of reflecting ![]() about the real axis. Also
about the real axis. Also ![]() represents the result of
reflecting
represents the result of
reflecting ![]() through the origin.
through the origin.
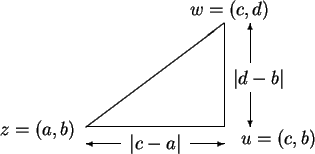
If ![]() and
and ![]() are two points in
are two points in
![]() , and
, and ![]() , then
, then ![]() are
the vertices of a right triangle having legs of length
are
the vertices of a right triangle having legs of length ![]() , and
, and ![]() . By the
Pythagorean theorem, the distance from
. By the
Pythagorean theorem, the distance from ![]() to
to ![]() is
is
![]() .
Also,
.
Also,
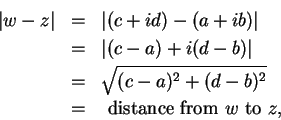
Claim: If
![]() , then
, then ![]() is the fourth vertex of the parallelogram having
consecutive vertices
is the fourth vertex of the parallelogram having
consecutive vertices ![]() .
.
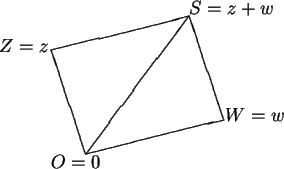
To make this look like a geometry proof, I'll denote points by upper case letters,
and let ![]() denote the distance from
denote the distance from ![]() to
to ![]() . Let
. Let ![]() ,
, ![]() ,
, ![]() ,
,
![]() . Then
. Then
We can now give a geometrical interpretation for the triangle inequality
(which
motivates its name). In the figure above,
It was the habit of the Epicureans, says Proclus ...to ridicule this theorem as being evident even to an ass, and requiring no proof, and their allegation that the theorem was `` known"even to an ass was based on the fact that, if fodder is placed at one angular point and the ass at another, he does not, in order to get his food, traverse the two sides of the triangle but only the one side separating them [19, vol. I page 287].
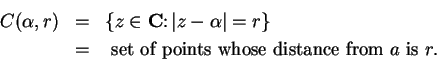
Proof: Let
![]() ; i.e.,
; i.e.,
![]() . Then
. Then
![]() , so
, so
![]() .
.
![]()
We can also give a geometrical interpretation to the product of two complex numbers.
Let ![]() and
and ![]() be complex numbers and let
be complex numbers and let ![]() . Let
. Let ![]() and let
and let ![]() .
.
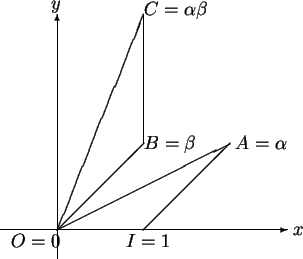
Then ![]() is similar to
is similar to ![]() . The proof consists in showing
that
. The proof consists in showing
that
From the similarity of ![]() and
and ![]() , we have
, we have
![]() . In particular, if we take
. In particular, if we take
![]() , we get the picture
, we get the picture
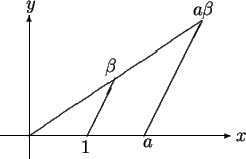
where
The figure below shows the powers of a complex number a.
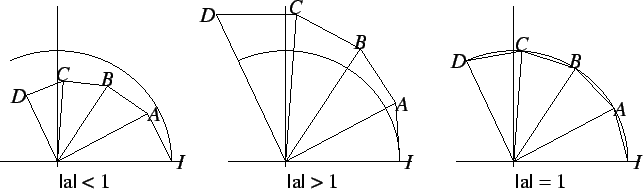
In each case the four triangles ![]() ,
, ![]() ,
,
![]() , and
, and ![]() are all similar. In the third figure,
where a is in the unit circle, the triangles
are all similar. In the third figure,
where a is in the unit circle, the triangles
![]() and
and ![]() are in fact congruent.
are in fact congruent.
If ![]() are points on the unit circle, then
are points on the unit circle, then
The previous geometrical argument suggests that