



Next: 12.3 Differentiation of Power
Up: 12. Power Series
Previous: 12.1 Definition and Examples
Index
12.8
Theorem.
Let
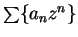 be a power
series. Suppose
be a power
series. Suppose
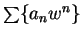 converges for some
converges for some
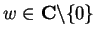 . Then
. Then
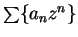 converges
absolutely for all
converges
absolutely for all 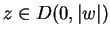 .
.
Proof: Since
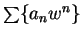 converges,
converges, 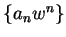 is a null sequence, and hence
is bounded. Say
is a null sequence, and hence
is bounded. Say
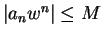 for all
for all
 . Let
. Let 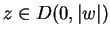 , so
, so
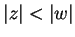 , and let
, and let
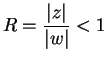 . Then for all
. Then for all

Now 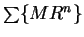 is a convergent geometric series, so by the comparison test,
is a convergent geometric series, so by the comparison test,
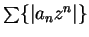 converges; i.e.,
converges; i.e.,
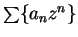 is absolutely convergent.
is absolutely convergent.

12.9
Corollary.
Let
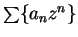 be a power series. Suppose
be a power series. Suppose
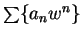 diverges for some
diverges for some
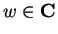 . Then
. Then
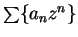 diverges for all
diverges for all
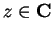 with
with 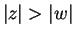 .
.
Proof: Suppose 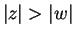 . If
. If
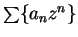 converges, then by the theorem,
converges, then by the theorem,
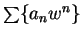 would also converge, contrary to our assumption.
would also converge, contrary to our assumption.

12.10
Theorem.
Let
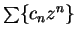 be a power series. Then one of the following three conditions
holds:
be a power series. Then one of the following three conditions
holds:
- a)
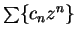 converges only when
converges only when 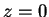 .
.
- b)
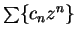 converges for all
converges for all
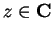 .
.
- c) There is a number
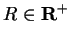 such that
such that
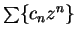 converges
absolutely for
converges
absolutely for 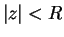 and diverges for
and diverges for 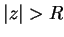 .
.
Proof: Suppose that neither a) nor b) is true. Then there are numbers
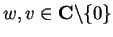 such that
such that
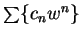 converges and
converges and
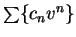 diverges. If
diverges. If
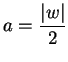 , and
, and 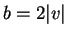 , it follows that
, it follows that
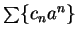 converges and
converges and
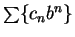 diverges. By a familiar procedure,
build a binary search sequence
diverges. By a familiar procedure,
build a binary search sequence ![$\{[a_k,b_k]\}$](img1730.gif) such that
such that ![$[a_0,b_0]$](img1731.gif)
![$=[a,b]$](img1732.gif) , and for
all
, and for
all
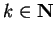 ,
,
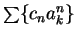 converges and
converges and
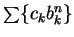 diverges. Let
diverges. Let
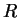 be the number such that
be the number such that
![$\{[a_k,b_k]\}\to R$](img1735.gif) . Then
. Then
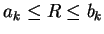 for all
for all
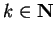 and
and
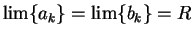 .
If
.
If 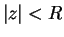 , then for some
, then for some
 we have
we have 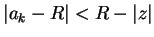 , and
, and
If 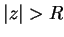 , then for some
, then for some
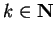 we have
we have 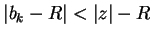 , and
, and
12.11
Definition (Radius of convergence.)
Let
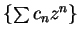
be a power series. If there is a number
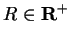
such that
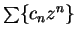
converges for
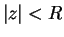
, and diverges for
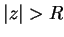
, we call
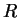
the
radius of convergence
of
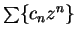
. If
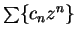
converges only
for
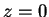
, we say
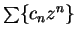
has radius of convergence
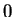
. If
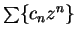
converges for all
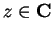
, we say
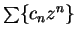
has radius of
convergence
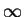
.
If a power series has radius of convergence
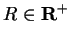 , I call
, I call 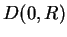 the disc of convergence for the series, and I call
the disc of convergence for the series, and I call 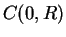 the circle of
convergence for the series. If
the circle of
convergence for the series. If 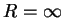 , I call
, I call
 the disc of convergence of
the series (even though
the disc of convergence of
the series (even though
 is not a disc).
is not a disc).
12.12
Example.
I will find the radius of convergence
for
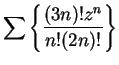
.
I will apply the ratio test. Since the ratio test applies to
positive sequences, I will consider absolute convergence.
Let
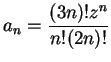
for all

.
Then for all
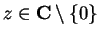
,
Hence
By the ratio test,
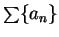
is absolutely convergent if
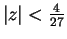
,
and is divergent if
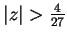
. It follows that the radius of
convergence for our series is
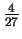
.
12.13
Exercise.
Find the radius of convergence
for the following power series:
- a)
-
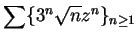 .
.
- b)
-
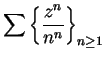 .
.




Next: 12.3 Differentiation of Power
Up: 12. Power Series
Previous: 12.1 Definition and Examples
Index
![]() converges,
converges, ![]() is a null sequence, and hence
is bounded. Say
is a null sequence, and hence
is bounded. Say
![]() for all
for all
![]() . Let
. Let ![]() , so
, so
![]() , and let
, and let
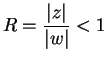 . Then for all
. Then for all
![]()
![]() . If
. If
![]() converges, then by the theorem,
converges, then by the theorem,
![]() would also converge, contrary to our assumption.
would also converge, contrary to our assumption.
![]()
![]() such that
such that
![]() converges and
converges and
![]() diverges. If
diverges. If
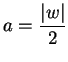 , and
, and ![]() , it follows that
, it follows that
![]() converges and
converges and
![]() diverges. By a familiar procedure,
build a binary search sequence
diverges. By a familiar procedure,
build a binary search sequence ![]() such that
such that ![]()
![]() , and for
all
, and for
all
![]() ,
,
![]() converges and
converges and
![]() diverges. Let
diverges. Let
![]() be the number such that
be the number such that
![]() . Then
. Then
![]() for all
for all
![]() and
and
![]() .
If
.
If ![]() , then for some
, then for some
![]() we have
we have ![]() , and
, and
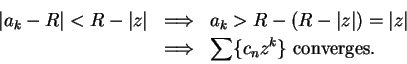
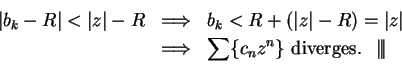
![]() , I call
, I call ![]() the disc of convergence for the series, and I call
the disc of convergence for the series, and I call ![]() the circle of
convergence for the series. If
the circle of
convergence for the series. If ![]() , I call
, I call
![]() the disc of convergence of
the series (even though
the disc of convergence of
the series (even though
![]() is not a disc).
is not a disc).
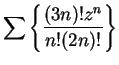 .
I will apply the ratio test. Since the ratio test applies to
positive sequences, I will consider absolute convergence.
Let
.
I will apply the ratio test. Since the ratio test applies to
positive sequences, I will consider absolute convergence.
Let
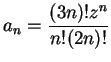 for all
for all
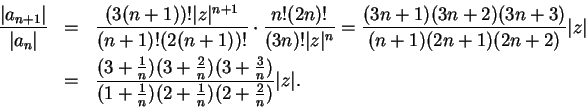
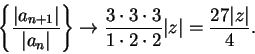
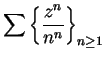 .
.