



Next: 8.3 Limits
Up: 8. Continuity
Previous: 8.1 Compositions with Sequences
Index
8.6
Definition (Continuous)
Let

be a complex function and let
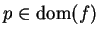
. We say
 is continuous
at
is continuous
at 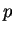
if
i.e., if
Let
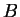
be a subset of

. We say
 is continuous on
is continuous on 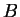
if

is
continuous at
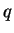
for all
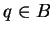
.
We say

is
continuous if

is
continuous on
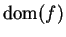
; i.e., if

is continuous at every point at which it is
defined.
8.7
Examples.
If
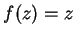
for all
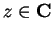
, then

is continuous. In this case
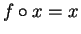
for
every sequence
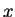
so the condition for continuity at
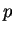
is
If
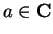
, then the constant function
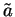
is continuous since for all
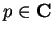
, and all complex sequences
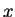
,
Notice that 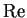 and
and 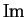 (Real part and imaginary part) are functions from
(Real part and imaginary part) are functions from
 to
to
 . In theorem 7.39 we showed if
. In theorem 7.39 we showed if 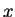 is any complex sequence and
is any complex sequence and
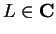 , then
, then
and
Hence
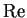
and
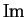
are continuous functions on

.
8.8
Theorem.
If
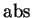 and
and
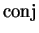 are functions from
are functions from
 to
to
 defined by
then
defined by
then
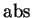 and
and
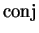 are continuous.
are continuous.
Proof: Let
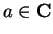 and let
and let 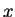 be any sequence in
be any sequence in
 such that
such that 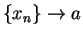 ;
i.e.,
;
i.e., 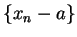 is a null sequence. By the reverse triangle inequality,
is a null sequence. By the reverse triangle inequality,
and
so we have
and hence
It follows by the comparison theorem that 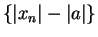 is a null sequence; i.e.,
is a null sequence; i.e.,
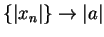 . Hence
. Hence
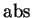 is continuous.
is continuous.
Since
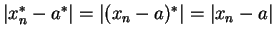 , the comparison theorem shows that
, the comparison theorem shows that
i.e.,
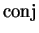 is continuous.
is continuous.

8.9
Example.
If
then

is not continuous at
, since
but
Notice that to show that a function

is
not continuous at a point

in its
domain, it is sufficient to find
one sequence
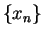
in
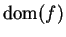
such that
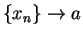
and either
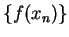
converges to a limit different from
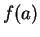
or
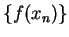
diverges.
8.10
Theorem (Sum and Product theorems.)
Let  be complex functions, and let
be complex functions, and let
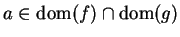 . If
. If  and
and  are continuous at
are continuous at  , then
, then 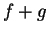 ,
, 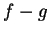 , and
, and 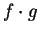 are continuous at
are continuous at  .
.
Proof: Let 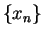 be a sequence in domain
be a sequence in domain 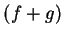 such that
such that 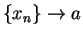 . Then
. Then
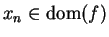 for all
for all 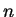 and
and
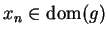 for all
for all 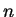 , and by continuity of
, and by continuity of  and
and  at
at  , it follows that
, it follows that
By the sum theorem for sequences,
Hence 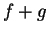 is continuous at
is continuous at  . The proofs of continuity for
. The proofs of continuity for 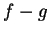 and
and 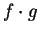 are similar.
are similar.
8.11
Theorem (Quotient theorem.)
Let  be complex functions and let
be complex functions and let
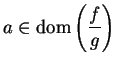 . If
. If
 and
and  are continuous at
are continuous at  , then
, then
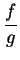 is continuous at
is continuous at  .
.
8.12
Exercise.
Prove the quotient theorem. Recall that
8.13
Theorem (Continuity of roots.)
Let
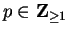 and let
and let
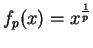 for all
for all
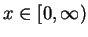 . Then
. Then 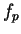 is continuous.
is continuous.
Proof: First we show 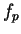 is continuous at
is continuous at 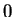 . Let
. Let 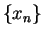 be a sequence in
be a sequence in
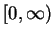 such that
such that 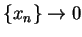 ; i.e., such that
; i.e., such that 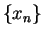 is a null sequence.
Then by the root theorem for null sequences (Theorem 7.19),
is a null sequence.
Then by the root theorem for null sequences (Theorem 7.19),
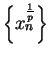 is a null sequence; i.e.,
is a null sequence; i.e.,
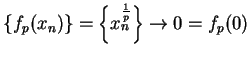 , so
, so 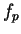 is
continuous at
is
continuous at  .
.
Next we show that 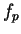 is continuous at
is continuous at 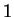 . By the formula for a finite
geometric series (3.72 ), we have for all
. By the formula for a finite
geometric series (3.72 ), we have for all
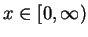
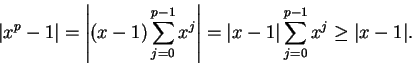 |
(8.14) |
If we replace 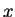 by
by 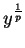 in (8.14), we get
in (8.14), we get
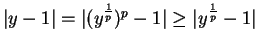 ,
i.e.,
,
i.e.,
Let 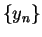 be a sequence in
be a sequence in 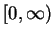 . Then
. Then
so
Hence 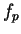 is continuous at
is continuous at 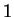 .
.
Finally we show that 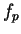 is continuous at arbitrary
is continuous at arbitrary
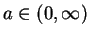 .
Let
.
Let
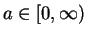 , and let
, and let 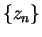 be a sequence n
be a sequence n 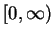 .
Then
.
Then
Thus 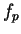 is continuous at
is continuous at  .
.

8.15
Definition (Composition of functions.)
Let
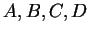
be sets, and let
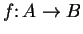
,
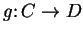
be functions. We
define a function
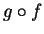
by the rules:
8.16
Examples.
Let
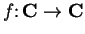
,
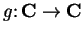
be defined by
Then
and
If
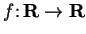 and
and
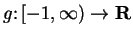 are defined by
are defined by
and
then
and
8.17
Theorem (Compositions of continuous functions.)
Let  be complex functions. If
be complex functions. If  is continuous at
is continuous at
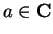 , and
, and  is
continuous at
is
continuous at 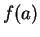 , then
, then 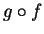 is continuous at
is continuous at  .
.
Proof: Let 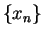 be a sequence in
be a sequence in
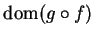 such that
such that 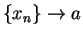 .
Then for all
.
Then for all
 , we have
, we have
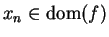 and
and
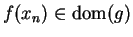 . By
continuity of
. By
continuity of  at
at  ,
,
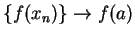 , and by continuity of
, and by continuity of  at
at 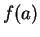 ,
,
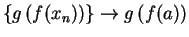 .
.

8.18
Example.
If
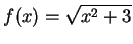
for all
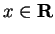
, then

is continuous (i.e.,

is
continuous at

for all
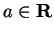
.)
8.19
Exercise.
A
Let
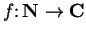
be defined
by
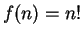
for all

. Is

continuous?




Next: 8.3 Limits
Up: 8. Continuity
Previous: 8.1 Compositions with Sequences
Index
![]() and
and ![]() (Real part and imaginary part) are functions from
(Real part and imaginary part) are functions from
![]() to
to
![]() . In theorem 7.39 we showed if
. In theorem 7.39 we showed if ![]() is any complex sequence and
is any complex sequence and
![]() , then
, then
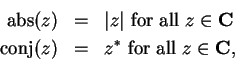
![]() and let
and let ![]() be any sequence in
be any sequence in
![]() such that
such that ![]() ;
i.e.,
;
i.e., ![]() is a null sequence. By the reverse triangle inequality,
is a null sequence. By the reverse triangle inequality,
![]() , the comparison theorem shows that
, the comparison theorem shows that
![]() be a sequence in domain
be a sequence in domain ![]() such that
such that ![]() . Then
. Then
![]() for all
for all ![]() and
and
![]() for all
for all ![]() , and by continuity of
, and by continuity of ![]() and
and ![]() at
at ![]() , it follows that
, it follows that
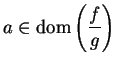 . If
. If
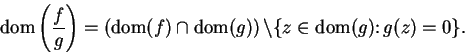
![]() is continuous at
is continuous at ![]() . Let
. Let ![]() be a sequence in
be a sequence in
![]() such that
such that ![]() ; i.e., such that
; i.e., such that ![]() is a null sequence.
Then by the root theorem for null sequences (Theorem 7.19),
is a null sequence.
Then by the root theorem for null sequences (Theorem 7.19),
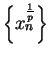 is a null sequence; i.e.,
is a null sequence; i.e.,
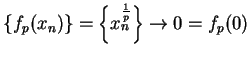 , so
, so ![]() is
continuous at
is
continuous at ![]() .
.
![]() is continuous at
is continuous at ![]() . By the formula for a finite
geometric series (3.72 ), we have for all
. By the formula for a finite
geometric series (3.72 ), we have for all
![]()
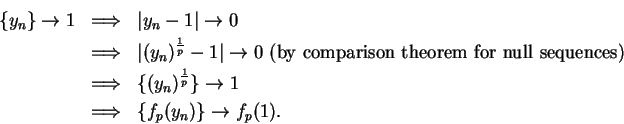
![]() is continuous at arbitrary
is continuous at arbitrary
![]() .
Let
.
Let
![]() , and let
, and let ![]() be a sequence n
be a sequence n ![]() .
Then
.
Then
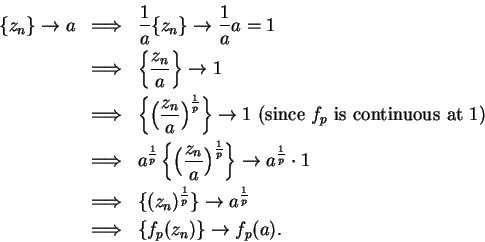
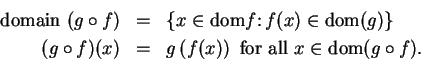
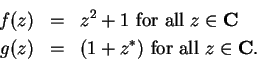
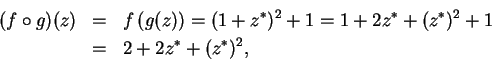
![]() and
and
![]() are defined by
are defined by
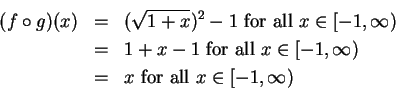
![]() be a sequence in
be a sequence in
![]() such that
such that ![]() .
Then for all
.
Then for all
![]() , we have
, we have
![]() and
and
![]() . By
continuity of
. By
continuity of ![]() at
at ![]() ,
,
![]() , and by continuity of
, and by continuity of ![]() at
at ![]() ,
,
![]() .
.
![]()