



Next: 9. Properties of Continuous
Up: 8. Continuity
Previous: 8.2 Continuity
Index
8.20
Definition (Limit point.)
Let

be a subset of

and let
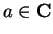
. We say

is a
limit point of

if there is a sequence

in
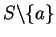
such that
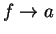
.
8.22
Exercise.
Supply the proof for Case 2 of example
8.21; i.e., show that
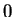
is
a limit point of
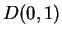
.
8.23
Example.
The set
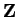
has no limit points. Suppose
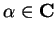
, and there is a sequence

in
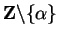
such that
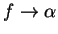
. Let
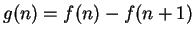
for
all

. By the translation thoerem
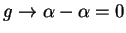
; i.e.,

is a
null sequence. Let
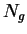
be a precision function for

. Then for all

,
Now
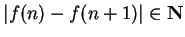
, so it follows that
and hence
This
contradicts the fact that
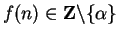
for all

.

8.24
Definition (Limit of a function.)
Let

be a complex function, and let

be a limit point of
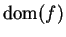
. We say
that
 has a limit at
has a limit at 
or that
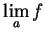 exists
exists if there exists a function
with
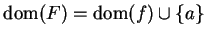
such that
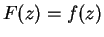
for all
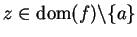
, and
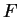
is continuous at

. In this case we denote the value of
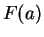
by
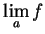
or
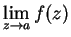
.
Theorem
8.30 shows that this definition makes sense. We will
give some examples before proving that theorem.
8.25
Warning.
Notice that
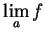
is defined only
when

is a limit point of
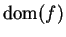
. For each complex number
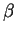
, define a function
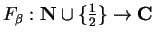
by
Then
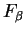
is continuous, and
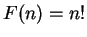
for all

.
If I did not put the requirement that

be a limit point of
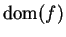
in the above definition, I'd have
I certainly do not want this to be the case.
8.26
Example.
Let
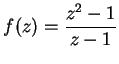
for all
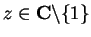
and let
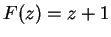
for all
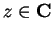
. Then
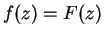
on
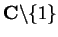
and
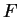
is
continuous at
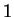
. Hence
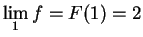
.
8.27
Example.
If
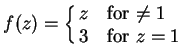
, then
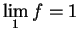
, since the function
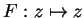
agrees with

on
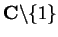
and is continuous at
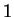
.
8.28
Example.
If

is continuous at

, and

is a limit point of domain

,
then

has a limit at

, and
8.29
Example.
Let
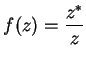
for all
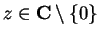
. Then

has no limit at
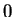
.
Proof: Suppose there were a continuous function 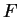 on
on
 such that
such that 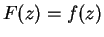 on
on
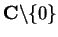 . Let
. Let
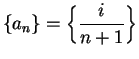 and
and
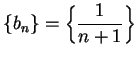 . Then
. Then 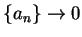 and
and 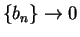 and so
and so
and also
Hence we get the contradiction 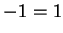 .
.

8.30
Theorem (Uniqueness of limits.)
Let  be a complex function, and let
be a complex function, and let  be a limit point of
be a limit point of
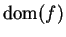 . Suppose
. Suppose
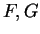 are two functions each having domain
are two functions each having domain
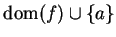 , and each continuous
at
, and each continuous
at  , and satisfying
, and satisfying 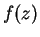
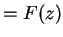
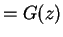 for all
for all
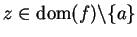 . Then
. Then
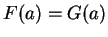 .
.
Proof: 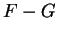 is continuous at
is continuous at  , and
, and 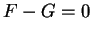 on
on
 . Let
. Let
 be a sequence in
be a sequence in
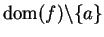 such that
such that 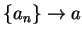 .
Since
.
Since 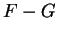 is continuous at
is continuous at  , we have
, we have
i.e.,
so 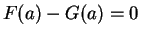 ; i.e.,
; i.e., 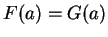 .
.

Proof: Suppose  has a limit at
has a limit at  , and let
, and let 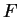 be a continuous function with
be a continuous function with
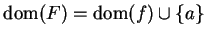 , and
, and 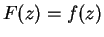 for all
for all
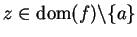 .
Let
.
Let 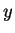 be a sequence in
be a sequence in
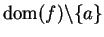 such that
such that 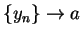 . Then
. Then
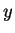 is a sequence in
is a sequence in
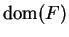 , so by continuity of
, so by continuity of 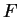 ,
,
Hence, condition (8.33) holds with 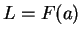 .
.
Conversely, suppose there is a number 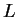 such that
such that
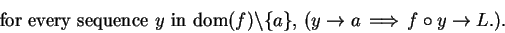 |
(8.34) |
Define
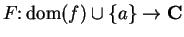 by
by
I need to show that 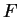 is continuous at
is continuous at  . Let
. Let 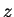 be a sequence in
be a sequence in
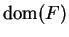 such that
such that 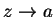 . I want to show that
. I want to show that 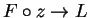 .
.
Let 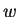 be a sequence in
be a sequence in
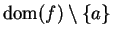 such that
such that
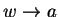 . (Such a sequence exists because
. (Such a sequence exists because  is a limit point of
is a limit point of
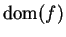 ). Define a sequence
). Define a sequence 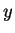 in
in
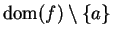 by
by
Let
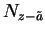 and
and
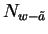 be precision functions
for
be precision functions
for 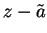 and
and 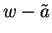 respectively. Let
respectively. Let
Then 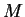 is a precision function for
is a precision function for 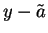 , since
for all
, since
for all
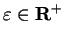 and all
and all
 ,
,
Hence 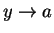 , and by assumption (8.34), it follows
that
, and by assumption (8.34), it follows
that
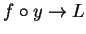 . I now claim that
. I now claim that
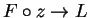 , and in fact any
precision function
, and in fact any
precision function 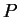 for
for
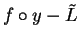 is a precision
function for
is a precision
function for
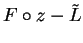 .
For all
.
For all
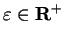 and all
and all
 ,
,
This completes the proof.

8.35
Example.
Let
I want to determine whether

has a limit at
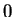
, i.e., I want to know whether there is a number
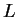
such that for every sequence
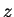
in
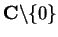
If
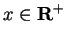
and
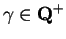
then
Since
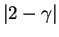
is either
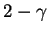
or
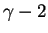
, we have
For each
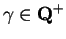
, define a sequence
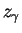
by
Then
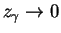
, and
Hence
It follows that

has no limit at
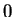
.
Let
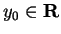 . It is clear that
. It is clear that  maps points on the horizontal line
maps points on the horizontal line 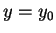 to
other points on the line
to
other points on the line 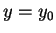 . I'll now look at the image of the parabola
. I'll now look at the image of the parabola
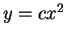 under
under  .
.
So

maps the right half of the parabola
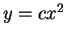
into the vertical line
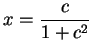
, and

maps the left half of the parabola to the line
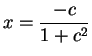
. Parabolas with
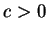
get mapped to the upper half
plane, and parabolas with
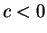
get mapped to the lower half plane. The
figure below
shows some parabolas and horizontal lines and their images under

.
8.36
Entertainment.
Explain how the cat's nose in the
above picture gets stretched, while its cheeks get pinched to a point.
(Hint: The figure shows the images of some parabolas
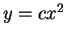
where
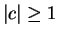
. What do the images of the parabolas
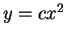
look
like when
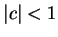
?)
8.37
Example.
It isn't quite true that `` the limit of the sum is the sum of the limits."
Let
Then from the continuity of the square root function and the composition theorem,
But
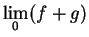
does not exist, since
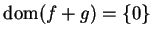
and
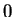
is not a limit
point of
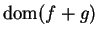
.
Proof: Suppose that
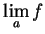 and
and
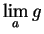 exist. Let
exist. Let 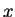 be any
sequence in
be any
sequence in
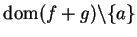 such that
such that 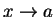 . Then
. Then 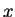 is a sequence
in both
is a sequence
in both
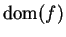 and
and
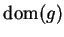 , so
, so
By the sum theorem for limits of sequences,
Hence 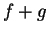 has a limit at
has a limit at  , and
, and
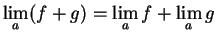 .
.
The other parts of the theorem are proved similarly, and the proofs are left to
you.

8.39
Exercise.
Prove the product theorem for limits; i.e., show that if

are complex
functions such that

and

have limits at
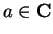
, and if

is a limit point
of
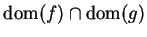
, then
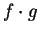
has a limit at

and
8.41
Examples.
The definition of bounded sequence given in
7.41 is a special case of the
definition just given for bounded function.
Let
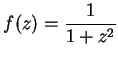 for all
for all
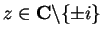 . Then
. Then  is
bounded on
is
bounded on
 since
since
However,

is not a bounded function, since
for all
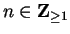
.
Let
(
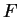
is the real part of the discontinuous function from example
8.35.)
I claim 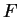 is bounded by
is bounded by 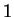 . For all
. For all
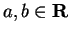 ,
,
(NOTE:
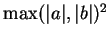
is either
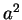
or
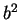
.) Hence if
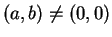
, then
To prove my claim, apply this result with
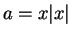
and
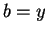
.
8.42
Exercise.
Show that
for all
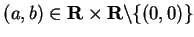
, and that equality holds if and only
if
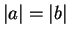
. (This shows that
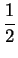
is a bound for the function
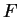
in
the previous example.) HINT: Consider
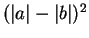
.




Next: 9. Properties of Continuous
Up: 8. Continuity
Previous: 8.2 Continuity
Index
![]() is a limit point of
is a limit point of
![]() .
.
![]() is a limit point of
is a limit point of ![]() .
Then there is a sequence
.
Then there is a sequence
![]() in
in
![]() such that
such that
![]() .
Since the absolute value function is continuous, it follows that
.
Since the absolute value function is continuous, it follows that
![]() . Since
. Since
![]() we know that
we know that
![]() (and hence
(and hence ![]() .) for all
.) for all
![]() . By the inequality
theorem for limits of sequences,
. By the inequality
theorem for limits of sequences,
![]() , i.e.
, i.e.
![]() .
.
![]() is a limit point
of
is a limit point
of ![]() .
.
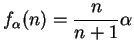 for all
for all
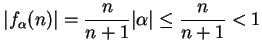 so
so
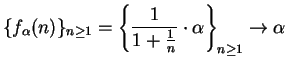 , so
, so 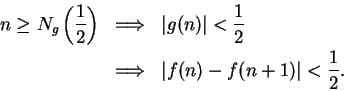
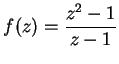 for all
for all
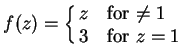 , then
, then
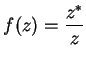 for all
for all
![]() on
on
![]() such that
such that ![]() on
on
![]() . Let
. Let
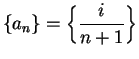 and
and
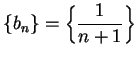 . Then
. Then ![]() and
and ![]() and so
and so
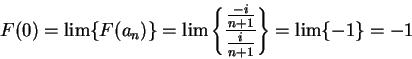
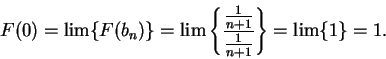
![]() is continuous at
is continuous at ![]() , and
, and ![]() on
on
![]() . Let
. Let
![]() be a sequence in
be a sequence in
![]() such that
such that ![]() .
Since
.
Since ![]() is continuous at
is continuous at ![]() , we have
, we have
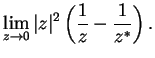
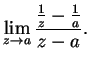 (Here
(Here
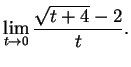
![]() has a limit at
has a limit at ![]() , and let
, and let ![]() be a continuous function with
be a continuous function with
![]() , and
, and ![]() for all
for all
![]() .
Let
.
Let ![]() be a sequence in
be a sequence in
![]() such that
such that ![]() . Then
. Then
![]() is a sequence in
is a sequence in
![]() , so by continuity of
, so by continuity of ![]() ,
,
![]() such that
such that
![]() be a sequence in
be a sequence in
![]() such that
such that
![]() . (Such a sequence exists because
. (Such a sequence exists because ![]() is a limit point of
is a limit point of
![]() ). Define a sequence
). Define a sequence ![]() in
in
![]() by
by
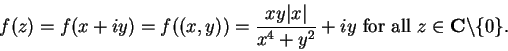
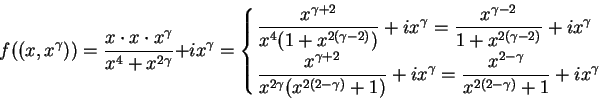
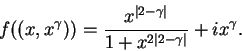
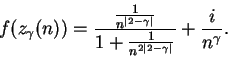
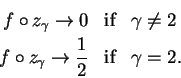
![]() . It is clear that
. It is clear that ![]() maps points on the horizontal line
maps points on the horizontal line ![]() to
other points on the line
to
other points on the line ![]() . I'll now look at the image of the parabola
. I'll now look at the image of the parabola
![]() under
under ![]() .
.
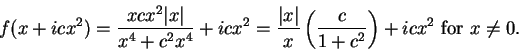
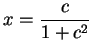 , and
, and 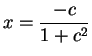 . Parabolas with
. Parabolas with 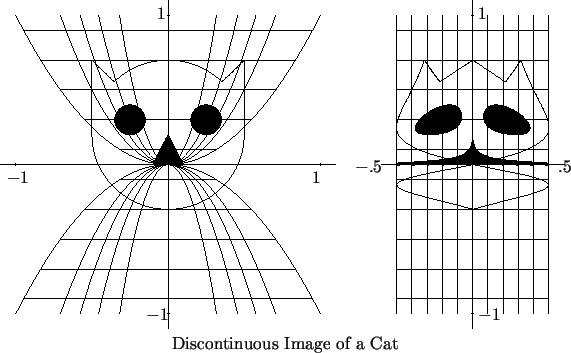
![\begin{eqnarray*}
f(x)&=&\sqrt x \mbox{ for } x\in [0,\infty) \\
g(x)&=&\sqrt{-x} \mbox{ for } x\in (-\infty,0].\\
\end{eqnarray*}](img839.gif)
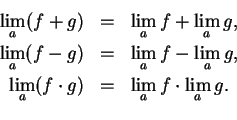
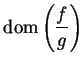 and
and
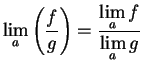 .
.
![]() and
and
![]() exist. Let
exist. Let ![]() be any
sequence in
be any
sequence in
![]() such that
such that ![]() . Then
. Then ![]() is a sequence
in both
is a sequence
in both
![]() and
and
![]() , so
, so
![]()
![]() is a functiom from some set
is a functiom from some set ![]() to
to
![]() and
and ![]() is a
subset of
is a
subset of ![]() . We say
. We say ![]() is bounded on
is bounded on ![]() if
if ![]() is a bounded set, and
any bound for
is a bounded set, and
any bound for ![]() is called a bound for
is called a bound for ![]() on
on ![]() . Thus a number
. Thus a number
![]() is a bound for
is a bound for ![]() on
on ![]() if and only if
if and only if
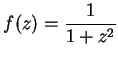 for all
for all
![]() . Then
. Then ![]() is
bounded on
is
bounded on
![]() since
since
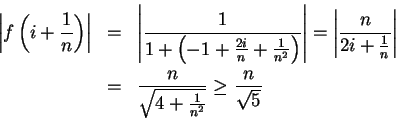
![]() is bounded by
is bounded by ![]() . For all
. For all
![]() ,
,
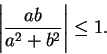
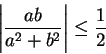
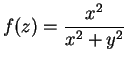 for all
for all
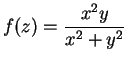 for all
for all
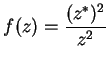 for all
for all
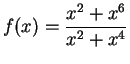 for all
for all
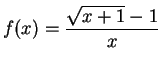 for all
for all