Proof: ![]()
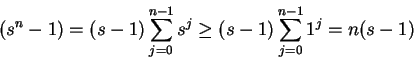
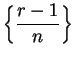 is a null sequence, it follows from the
comparison theorem for null sequences that
is a null sequence, it follows from the
comparison theorem for null sequences that
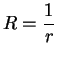 . Then
. Then 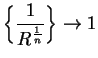 ; i.e.,
; i.e.,
We have shown that the theorem holds in all cases.
![]()
Proof: The last assertion was shown in theorem 7.7, and the second
statement is clear, and it is also clear that
![]() if
if ![]() .
.
Suppose that ![]() .
I will show that
.
I will show that
To prove (7.65),
let ![]() be a precision function for
be a precision function for
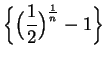 ,
and let
,
and let
![]() .
Then
.
Then
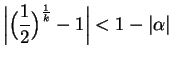 , so
, so
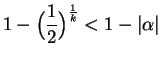 ,
so
,
so
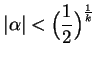 .
and hence
.
and hence
![]() , which is what we wanted to show.
, which is what we wanted to show.
![]()
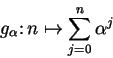
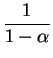 . If
. If
Proof: We saw in theorem 3.71
that
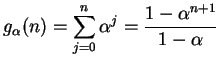 for all
for all
![]() . If
. If ![]() ,
,
![]() . This sequence diverges, since it
is not bounded. If
. This sequence diverges, since it
is not bounded. If ![]() , then by the previous theorem
, then by the previous theorem
![]() , so
, so
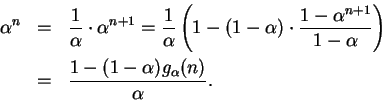
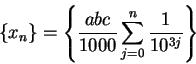
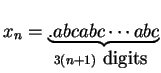 .
Then
.
Then 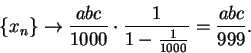
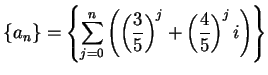 .
Does
.
Does 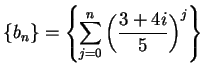 . Does
. Does 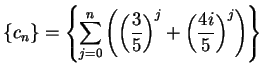 . Does
. Does
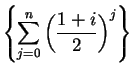 and
and
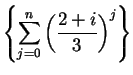 (which are drawn above in figure b 7.1) converge,
and that
the limits appear to be in agreement with Figure b above.
(which are drawn above in figure b 7.1) converge,
and that
the limits appear to be in agreement with Figure b above.
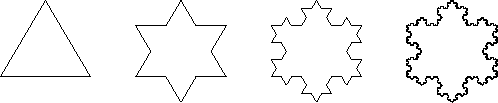
area ![]() , and side
, and side ![]() . Note that an
equilateral triangle with side
. Note that an
equilateral triangle with side
![]() has area
has area
![]() .
Starting with
.
Starting with ![]() , we will now construct a sequence
, we will now construct a sequence ![]() of polygons.
of polygons. ![]() will have
will have ![]() sides, all having length
sides, all having length
![]() . We let
. We let
![]() (so
(so ![]() has
has ![]() sides of length
sides of length
![]() ). To
construct
). To
construct ![]() from
from ![]() we attach an equilateral triangle with side
of length
we attach an equilateral triangle with side
of length
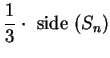 to the middle third of each side of
to the middle third of each side of ![]() .
.
A horizontal side
![]() of
of ![]() might be replaced by
might be replaced by
![]() .
Each side of
.
Each side of ![]() is replaced by 4
sides of length
is replaced by 4
sides of length
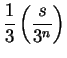 , so
, so ![]() will have
will have
![]() sides of length
sides of length
![]() . The figure
shows some of these polygons. I will call the polygons
. The figure
shows some of these polygons. I will call the polygons ![]() snowflake
polygons.
We have
snowflake
polygons.
We have
![]() for all
for all ![]() . The snowflake
. The snowflake ![]() is the
union of all of the sets
is the
union of all of the sets ![]() ; i.e., a point
; i.e., a point ![]() is in
is in ![]() if and only if it is in
if and only if it is in ![]() for some
for some
![]() .
.
Find the area of ![]() (in terms of the area
(in terms of the area ![]() of
of ![]() ), for example
), for example