



Next: 7.2 Convergence
Up: 7. Complex Sequences
Previous: 7. Complex Sequences
Index
In definition 5.1 ,
we defined a sequence in
 to be a function
to be a function
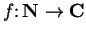 . Since we are identifying
. Since we are identifying
 with a subset of
with a subset of
 , every
sequence in
, every
sequence in
 is also a sequence in
is also a sequence in
 , and all of our results for complex
sequences are applicable to real sequences.
, and all of our results for complex
sequences are applicable to real sequences.
7.1
Notation (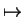 )
)
I will say `` consider the sequence
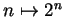
" or `` consider the
sequence
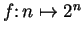
" to mean `` consider the sequence
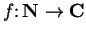
such that
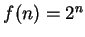
for all

". The arrow
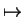
is
read `` maps to".
7.2
Definition (Geometric sequence.)
For each
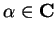
, the sequence
is called the
geometric sequence with ratio 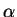
.
I will often represent a sequence  in
in
 by a polygonal line with vertices
by a polygonal line with vertices
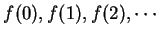 .
The two figures below represent geometric sequences with
ratios
.
The two figures below represent geometric sequences with
ratios
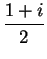 and
and
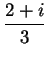 respectively.
respectively.
7.3
Definition (Geometric series.)
If
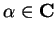
, then the sequence
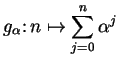
is called the
geometric series with ratio
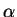
.
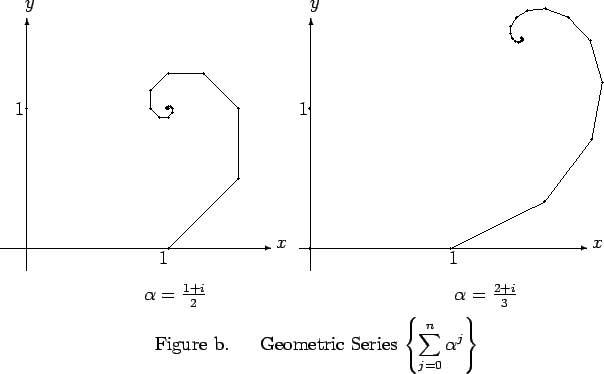
Figure b shows the geometric series corresponding to the geometric sequences
in figure a. If you examine the figures you should notice a remarkable
similarity between the figure representing 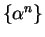 and the figure representing
and the figure representing
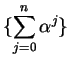 .
.
7.4
Entertainment.
Describe the apparent similarity between the figure for
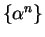
and the
figure for
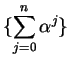
. Then prove that this similarity is
really present for all
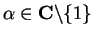
.
7.5
Definition (Constant sequence.)
For each
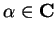
, let
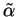
,
denote the constant sequence
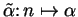
; i.e.,
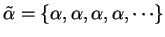
.




Next: 7.2 Convergence
Up: 7. Complex Sequences
Previous: 7. Complex Sequences
Index
![]() in
in
![]() by a polygonal line with vertices
by a polygonal line with vertices
![]() .
The two figures below represent geometric sequences with
ratios
.
The two figures below represent geometric sequences with
ratios
![]() and
and
![]() respectively.
respectively.

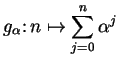 is called the geometric series with ratio
is called the geometric series with ratio
![]() and the figure representing
and the figure representing
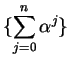 .
.
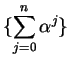 . Then prove that this similarity is
really present for all
. Then prove that this similarity is
really present for all