We denote the set of integers in
Proof:
Now suppose
![]() . Then
. Then ![]() where
where
![]() . If
. If ![]() , then
, then
![]() . If
. If ![]() , then
, then ![]() , so
, so
![]() , so
, so
![]() , so
, so
![]() , so
, so
![]() . Therefore,
. Therefore,
![]() or
or
![]() ; i.e.,
; i.e.,
![]() , so
, so
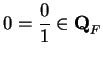 and
and
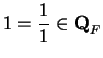 .
.
Proof: The various commutative, associative and distributive laws hold in
![]() ,
because they hold in
,
because they hold in ![]() , and we've noted that the additive and multiplicative
identities of
, and we've noted that the additive and multiplicative
identities of ![]() are in
are in
![]() , and they act as identities in
, and they act as identities in
![]() because they
are identities in
because they
are identities in ![]() . We note that
. We note that ![]() and
and ![]() define binary operations on
define binary operations on
![]() ; i.e., the sum and product of elements in
; i.e., the sum and product of elements in
![]() is in
is in
![]() . Let
. Let
![]() write
write
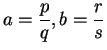 where
where
![]() and
and
![]() . Then
. Then
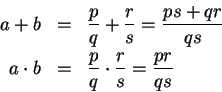
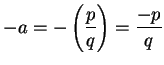 where
where
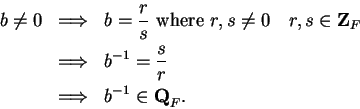
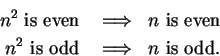
I want to show that in any ordered field ![]() ,
, ![]() is not a square in
is not a square in
![]() . To
show this I will use the following lemma.
. To
show this I will use the following lemma.
Proof: Let ![]() be an ordered field, and let
be an ordered field, and let
![]() . Then
. Then
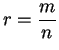 where
where
![]() and
and ![]() . Since
. Since
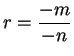 , we may assume
without loss of generality that
, we may assume
without loss of generality that ![]() .
Then
.
Then
![]() so we can write any element
of
so we can write any element
of
![]() in the form
in the form
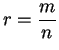 where
where
![]() ,
,
![]() and
and ![]() .
Let
.
Let
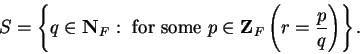
Proof: Suppose there were an element
![]() such that
such that ![]() . By our lemma,
we can write
. By our lemma,
we can write
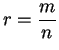 where
where
![]() ,
, ![]() not both even. Now
not both even. Now
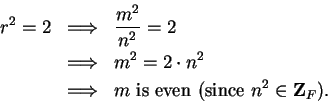
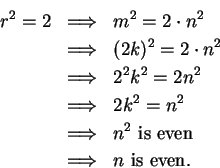
When Plato (427?-347B.C.) wrote The Laws, he lamented that most Greeks at the time believed that all numbers were rational (i.e. that all lines are commensurable):
ATHENIAN: My dear Cleinias, even I took a very long time to discover mankind's plight in this business; but when I did, I was amazed, and could scarcely believe that human beings could suffer from such swinish stupidity. I blushed not only for myself, but for Greeks in general.
CLEINIAS: Why so? Go on, sir, tell us what you're getting at.
ATHENIAN: The real relationship between commensurables and incommensurables. We must be very poor specimens if on inspection we can't tell them apart. These are the problems we ought to keep on putting up to each other, in a competitive spirit, when we've sufficient time to do them justice; and it's a much more civilized pastime for old men then draughts.
CLEINIAS: Perhaps so. Come to think of it, draughts is not radically different from such studies.
ATHENIAN: Well, Cleinias, I maintain that these subjects are what the younger generation should go in for. They do no harm, and are not very difficult: they can be learnt in play, and so far from harming the state, they'll do it some good[39, book vii,820].
However, when Aristotle (384-322 BC) wrote the Priora Analytica, he assumed that his reader was familiar with the proof of theorem 3.45 just given. The following quotation would not be understood by anyone who did not know that proof.
For all who effect an argument per impossible infer syllogistically what is false, and prove the initial conclusion hypothetically when something impossible results from the assumption of its contradictory; e.g., that the diagonal of the square is incommensurate with the side, because odd numbers are equal to evens if it is supposed to be commensurate. One infers syllogistically that odd numbers come out equal to evens, and one proves hypothetically the incommensurability of the diagonal since a falsehood results through contradicting this.[4, 1-23, 41a, 23-31]
The meaning of the word ``rational'' has changed since the time of Euclid.
He would have said that a line of length ![]() was rational, but a rectangle of area
was rational, but a rectangle of area ![]() was irrational.
The following quotation is from book X of
The Elements[19, vol 3, p10, definitions 3 and 4].
was irrational.
The following quotation is from book X of
The Elements[19, vol 3, p10, definitions 3 and 4].
Let then the assigned straight line be called rational, and those straight lines which are commensurable with it, whether in length and in square or in square only, rational, but those which are incommensurable with it irrational.
4. And let the square on the assigned straight line be called rational, and those areas which are commensurable with it rational, but those which are incommensurable with it irrational.
everything irrational and formless is properly concealed, and, if any soul should rashly invade this region of life and lay it open, it would be carried away into the sea of becoming and be overwhelmed by its unresting currents.
However, one can also construct ordered fields ![]() and
and ![]() such that
such that
![]() and
and
![]() are radically different! (see [41]) The reason that both of these
apparently contradictory things can happen is that our definition of
are radically different! (see [41]) The reason that both of these
apparently contradictory things can happen is that our definition of
![]() involves
looking at the set of all inductive subsets of
involves
looking at the set of all inductive subsets of ![]() , and our vague notions of set and
function are just too imprecise to deal with this delicate question. The two quoted
contradictory results are proved using different set theories, which are not
consistent with each other, but both of which are more or less consistent with
everything we've used about sets.
, and our vague notions of set and
function are just too imprecise to deal with this delicate question. The two quoted
contradictory results are proved using different set theories, which are not
consistent with each other, but both of which are more or less consistent with
everything we've used about sets.