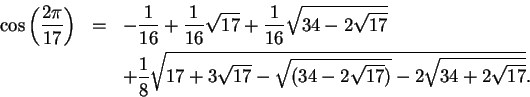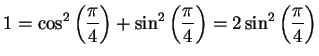 , and hence
, and hence
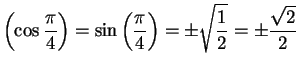 . Since we know
. Since we know
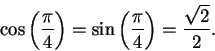
Observe that if
![]() , then the problem of
calculating
, then the problem of
calculating ![]() and
and ![]() is
the same as the problem of calculating
is
the same as the problem of calculating ![]() . Let
. Let
![]() . We know that the
complex solutions of
. We know that the
complex solutions of ![]() are
are
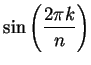 and
and
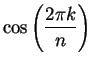 in algebraic terms. We have
in algebraic terms. We have
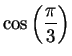 and
and
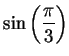 .
.
The numbers
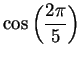 and
and
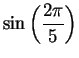 can also be
expressed algebraically.
can also be
expressed algebraically.
If
![]() , then
, then ![]() , so
, so
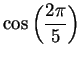 satisfies a quadratic equation.
satisfies a quadratic equation.
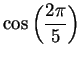 and
and
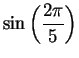 in algebraic terms.
in algebraic terms.
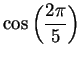 . What is the geometrical significance of the other solution?
. What is the geometrical significance of the other solution?
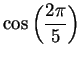 shows that
a regular pentagon can be inscribed in a given circle. Let a circle be given, and
call its radius
shows that
a regular pentagon can be inscribed in a given circle. Let a circle be given, and
call its radius 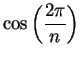 with compass
and straightedge (see the figure), then you can construct a side of a regular
with compass
and straightedge (see the figure), then you can construct a side of a regular
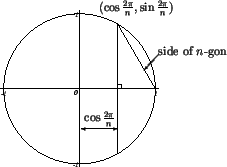
For example, since
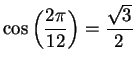 , we
can construct a dodecagon as follows:
, we
can construct a dodecagon as follows:
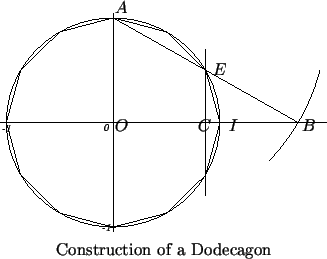
In the figure, make an arc of radius ![]() with center at
with center at ![]() , intersecting the
, intersecting the
![]() -axis at
-axis at ![]() . Then
. Then ![]() , so if
, so if ![]() bisects
bisects ![]() , then
, then
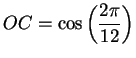 , and the vertical line through
, and the vertical line through ![]() intersects the circle at
intersects the circle at ![]() where
where ![]() is a side of the
is a side of the ![]() -gon.
-gon.
Use the formula for
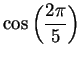 to inscribe a regular
pentagon in a circle.
to inscribe a regular
pentagon in a circle.
Gauss discovered this result in 1796 [31, p 754] when he was a nineteen year old student at Göttingen. The result is [21, p 458]