



Next: 12.6 Trigonometric Functions
Up: 12. Power Series
Previous: 12.4 The Exponential Function
Index
12.37
Definition (Logarithm.)
Let
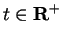
. The
logarithm of 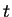
is the unique number
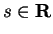
such that
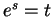
. We denote the logarithm of
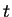
by
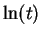
, Hence
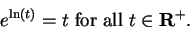 |
(12.38) |
12.39
Remark.
Since
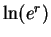
is the unique number
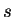
such that
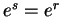
, it follows that
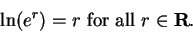 |
(12.40) |
12.41
Theorem.
For all
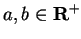 ,
,
Proof:
12.43
Remark.
It follows from the fact that
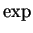
is strictly increasing on

that
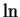
is
strictly increasing on
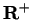
: if
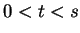
, then both of the statements
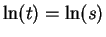
and
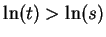
lead to contradictions.
12.44
Theorem (Continuity of 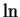 .)
.)
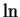 is a continuous function on
is a continuous function on
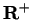 .
.
Proof: Let
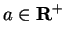 , and let
, and let  be a sequence in
be a sequence in
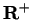 such that
such that
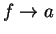 . I want to show that
. I want to show that
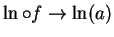 . Let
. Let
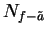 be a precision function for
be a precision function for 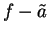 .
I want to construct a precision function
.
I want to construct a precision function 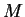 for
for
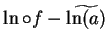 .
.
Scratchwork: For all
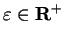 , and all
, and all
 ,
,
Note that since 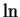 is strictly increasing,
is strictly increasing,
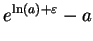 and
and
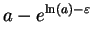 are both positive. This calculation
motivates the following definition:
are both positive. This calculation
motivates the following definition:
For all
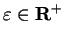 , let
, let
Then for all
 ,
,
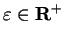 ,
,
Hence 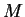 is a precision function for
is a precision function for
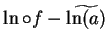 .
.

12.45
Theorem (Differentiability of 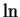 .)The function
.)The function 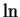 is differentiable on
is differentiable on
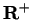 and
and
Proof: Let
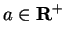 and let
and let 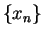 be a sequence in
be a sequence in
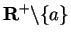 .
Then
.
Then
(Note, I have not divided by 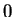 .) Since
.) Since 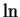 is continuous, I know
is continuous, I know
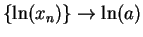 , and hence
, and hence
Hence,
i.e.,
This shows that
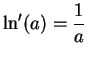 .
.




Next: 12.6 Trigonometric Functions
Up: 12. Power Series
Previous: 12.4 The Exponential Function
Index
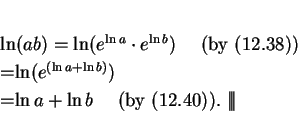
![]() , and let
, and let ![]() be a sequence in
be a sequence in
![]() such that
such that
![]() . I want to show that
. I want to show that
![]() . Let
. Let
![]() be a precision function for
be a precision function for ![]() .
I want to construct a precision function
.
I want to construct a precision function ![]() for
for
![]() .
.
![]() , and all
, and all
![]() ,
,
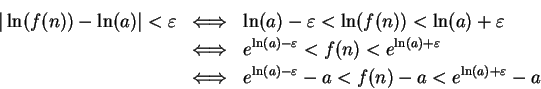
![]() , let
, let
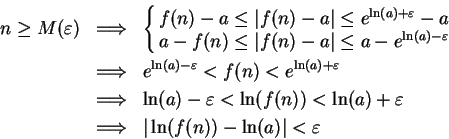
![]() and let
and let ![]() be a sequence in
be a sequence in
![]() .
Then
.
Then
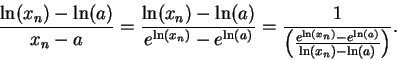
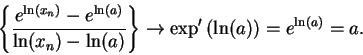
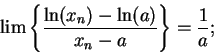
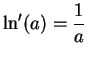 .
.