4.2 Complex Conjugate.

4.21   Definition (Complex conjugate.) Let $F$ be a field in which $-1$ is not a square. Let $z=(a,b)=a+bi$ be an element of $\mbox{{\bf C}}_F$. We define

$$z^*=(a,-b)=a-bi.$$

$z^*$ is called the conjugate of $z$.

The following remark will be needed somewhere in the proof of the next exercise.

4.22   Remark. If $F$ is a field in which $-1$ is not a square, then $2\neq 0$ in $F$, since

$$\begin{eqnarray*} 2=0 &\mbox{$\Longrightarrow$}&1+1=0 \\ &\mbox{$\Longrightarro... ...$}&-1=1^2 \\ &\mbox{$\Longrightarrow$}&-1 \mbox{ is a square }. \end{eqnarray*}$$

4.23   Exercise. A Let $F$ be a field in which $-1$ is not a square. Let $z,w\in\mbox{{\bf C}}_F$. Show that

a)

$(z+w)^*=z^*+w^*$.

b)

$(z\cdot w)^*=z^*\cdot w^*$.

c)

$${ \left({z\over w}\right)^*={{z^*}\over {w^*}}}$$ if $w\neq 0$.

d)

$z^*=0\hspace{1ex}\Longleftrightarrow\hspace{1ex}z=0$.

e)

If $z=a+bi\in\mbox{{\bf C}}_F$, then $zz^*=a^2+b^2 \in F$. If $z\neq 0$ then $zz^*\neq 0$.

f)

$z^*=z\hspace{1ex}\Longleftrightarrow\hspace{1ex}z\in F$.

g)

$z^{**} =z$.

4.24   Example. The results of the previous exercise provide a way to write expressions of the form $${{z\over w}}$$ in the form $a+bi$. Write

$${z\over w}={z\over w}\cdot {{w^*}\over {w^*}}$$

and calculate away. For example, in $\mbox{{\bf C}}_{\mathbf{Q}}$, we have

$$\begin{eqnarray*} {{2+i}\over {(3-i)(4+5i)}}&=&{{(2+i)}\over {(3-i)(4+5i)}}\cdot... ...{5(9-i)}\over {5\cdot 82}} \\ &=& {9\over {82}}-{1\over {82}}i. \end{eqnarray*}$$

4.25   Exercise. A Write each of the following elements of $\mbox{{\bf C}}_{\mathbf{Q}}$ in the form $a+bi$ where $a,b\in\mbox{{\bf Q}}$.

a)

$${ {{(4-2i)(1+2i)}\over {(1-3i)(-1+3i)}}}$$

b)

$(1+i)^{10}$

4.26   Note. The first appearance of complex numbers is in Ars Magna (1545) by Girolamo Cardano (1501-1576).

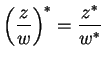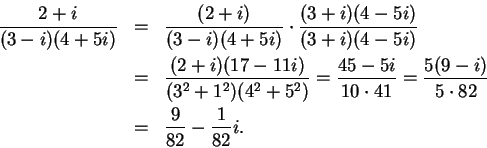
If it should be said, Divide 10 into two parts the product of which is 30 or 40, it is clear that this case is impossible. Nevertheless, we will work thus: $\cdots$ [16, page 219].

He then proceeds to calculate that the parts are $${5+\sqrt{-15}}$$ and $${5-\sqrt{-15}}$$, and says

Putting aside the mental tortures involved, multiply $${5+\sqrt{-15}}$$ by $5-\sqrt{-15}$ making $25-(-15)$ which is $+15$. Hence this product is 40 $\cdots$. So progresses arithmetic subtlety the end of which, as is said, is as refined as it is useless [16, page 219-220].

Around 1770, Euler wrote

144. All such expressions as $\sqrt{-1}, \sqrt{-2}, \sqrt{-3}, \sqrt{-4}, \&c$ are consequently impossible, or imaginary numbers, since they represent roots of negative quantities; and of such numbers we may truly assert that they are neither nothing nor greater than nothing, nor less than nothing; which necessarily constitutes them imaginary, or impossible.

145. But notwithstanding this, these numbers present themselves to the mind; they exist in our imagination, and we still have a sufficient idea of them; since we know that by $\sqrt{-4}$ is meant a number which, multiplied by itself, produces $-4$; for this reason also, nothing prevents us from making use of these imaginary numbers, and employing them in calculation. [20, p 43]

The use of the letter $i$ to represent $\sqrt{-1}$ was introduced by Euler in 1777.[15, vol 2, p 128] Both Maple and Mathematica use I to denote $\sqrt{-1}$.

The first attempts to ``justify'' the complex numbers appear around 1800. The early descriptions were geometrical rather than algebraic. The algebraic construction of $\mbox{{\bf C}}_F$ used in these notes follows the ideas described by William Hamilton circa 1835 [25, page 83].

You will often find the complex conjugate of $z$ denoted by $\overline{z}$ instead of $z^*$. The notion of complex conjugate seems to be due to Cauchy[45, page 26], who called $a+bi$ and $a-bi$ conjugates of each other.