



Next: 9.2 Intermediate Value Theorem
Up: 9. Properties of Continuous
Previous: 9. Properties of Continuous
Index
9.1
Definition (Maximum, Minimum.)
Let
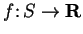
be a function from a set

to

, and let
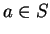
. We
say that
 has a maximum at
has a maximum at 
if
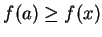
for all
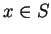
, and we
say
 has a minimum at
has a minimum at 
if
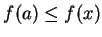
for all
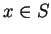
.
9.2
Definition (Maximizing set.)
Let
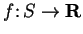
be a function and let
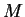
be a subset of

. We say
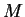
is a
maximizing set for

on

if for each
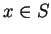
there is a point
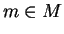
such that
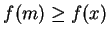
.
9.3
Examples.
If

has a maximum at

then
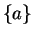
is a maximizing set for

on

.
If 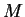 is a maximizing set for
is a maximizing set for  on
on  , and
, and
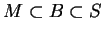 , then
, then 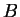 is
also a maximizing set for
is
also a maximizing set for  on
on  .
.
If
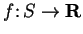 is any function (with
is any function (with
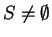 ), then
), then  is a
maximizing set for
is a
maximizing set for  on
on  , so every function with non-empty domain has a
maximizing set.
, so every function with non-empty domain has a
maximizing set.
Let
Then every disc
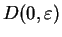
is a maximizing set for

, since if
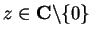
we can find

with
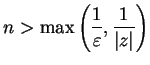
; then
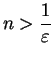
, so
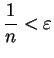
, so
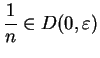
and
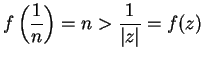
. This argument shows that
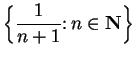
is also a maximizing set for

.
9.4
Remark.
Let

be a set, and let
, and let
be a subset of

. If
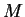
is
not a maximizing set for

on

, then there is some point
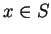
such
that
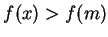
for all
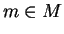
.
9.5
Lemma.
Let  be a set, let
be a set, let
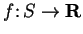 be a function, and let
be a function, and let 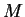 be a maximizing
set for
be a maximizing
set for  on
on  . If
. If 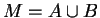 , then at least one of
, then at least one of 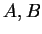 is a maximizing set
for
is a maximizing set
for  on
on  .
.
Proof: Suppose 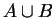 is a maximizing set for
is a maximizing set for  on
on  , but
, but 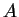 is not a
maximizing set for
is not a
maximizing set for  on
on  . Then there is some
. Then there is some 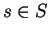 such that for all
such that for all 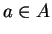 ,
, 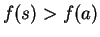 . Since
. Since 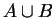 is a maximizing set for
is a maximizing set for  on
on  ,
there is an element
,
there is an element 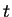 in
in 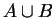 such that
such that 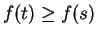 , so
, so 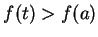 for all
for all 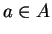 , so
, so 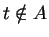 , so
, so 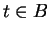 . Now, for every
. Now, for every 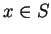 there is an element
there is an element 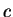 in
in 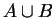 with
with
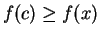 . If
. If 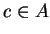 , then the element
, then the element 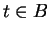 satisfies
satisfies
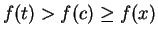 so
there is some element
so
there is some element 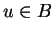 with
with 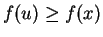 (if
(if 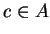 , take
, take 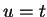 ;
if
;
if 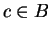 , take
, take 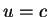 .) Hence
.) Hence 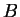 is a
maximizing set for
is a
maximizing set for  on
on  .
.

9.6
Theorem (Extreme value theorem.)
Let
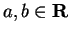 with
with 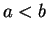 and let
and let
![$f\colon [a,b]\to\mbox{{\bf R}}$](img934.gif) be a continuous function.
Then
be a continuous function.
Then  has a maximum and a minimum on
has a maximum and a minimum on ![$[a,b]$](img935.gif) .
.
Proof: We will construct a binary search sequence ![$\{[a_n,b_n]\}$](img492.gif) with
with
![$[a_0,b_0]=[a,b]$](img936.gif) such that each interval
such that each interval ![$[a_n,b_n]$](img937.gif) is a maximizing set for
is a maximizing set for  on
on
![$[a,b]$](img935.gif) . We put
. We put
By the preceding lemma (and induction), we see that each interval ![$[a_n,b_n]$](img937.gif) is a
maximizing set for
is a
maximizing set for  on
on ![$[a,b]$](img935.gif) . Let
. Let 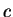 be the number such that
be the number such that
![$\{[a_n,b_n]\} \to c$](img493.gif) and let
and let ![$s\in [a,b]$](img939.gif) . Since
. Since ![$[a_n,b_n]$](img937.gif) is a maximizing set for
is a maximizing set for  on
on ![$[a,b]$](img935.gif) ,
there is a number
,
there is a number
![$s_n\in[a_n,b_n]$](img940.gif) with
with
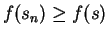 . Since
. Since
we have
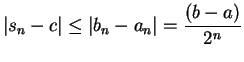 , so
, so 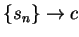 . By
continuity of
. By
continuity of  ,
,
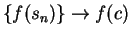 . Since
. Since
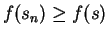 , it follows by the
inequality theorem for limits that
, it follows by the
inequality theorem for limits that
Hence 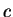 is a maximum point for
is a maximum point for  on
on ![$[a,b]$](img935.gif) . This shows that
. This shows that  has a
maximum. Since
has a
maximum. Since 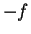 is also a continuous function on
is also a continuous function on ![$[a,b]$](img935.gif) ,
, 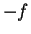 has a maximum on
has a maximum on
![$[a,b]$](img935.gif) ; i.e., there is a point
; i.e., there is a point ![$p\in [a,b]$](img948.gif) such that
such that
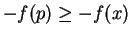 for all
for all
![$x\in [a,b]$](img950.gif) . Then
. Then 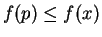 for all
for all ![$x\in [a,b]$](img950.gif) , so
, so  has a minimum at
has a minimum at
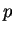 .
.

9.7
Definition (Upper bound.)
Let

be a subset of

, let
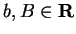
.
We say
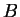
is an
upper bound
for

if
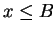
for all
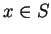
, and we say
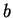
is a
lower bound for

if
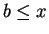
for all
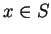
.
9.8
Remark.
If

is a bounded subset of
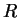
and
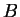
is a bound for

, then
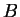
is an upper
bound for

and
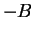
is a lower bound for

, since
Conversely, if a subset

of

has an upper bound
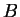
and a lower bound
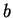
,then

is bounded, and
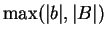
is a bound for

, since
9.9
Theorem (Boundedness theorem.)
Let
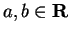 with
with 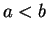 and let
and let
![$f\colon [a,b]\to\mbox{{\bf R}}$](img934.gif) be a continuous function.
Then
be a continuous function.
Then  is bounded on
is bounded on ![$[a,b]$](img935.gif) .
.
Proof: By the extreme value theorem, there are points ![$p,q\in[a,b]$](img961.gif) such that
such that
Hence ![$f([a,b])$](img963.gif) has an upper bound and a lower bound, so
has an upper bound and a lower bound, so ![$f([a,b])$](img963.gif) is bounded.
is bounded.

9.10
Exercise.
A
Give examples of the functions described below, or explain why no such function
exists.
Describe your functions by formulas if you can, but pictures
of graphs will do if a formula seems too complicated.
- a)
-
![$f\colon[0,1]\to\mbox{{\bf R}}$](img964.gif) ,
,  is not bounded.
is not bounded.
- b)
-
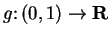 ,
,  is continuous,
is continuous,  is not bounded.
is not bounded.
- c)
-
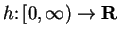 ,
, 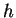 is continuous,
is continuous, 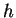 is not bounded.
is not bounded.
- d)
-
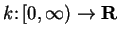 ,
, 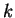 is strictly increasing,
is strictly increasing, 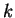 is continuous,
is continuous,
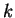 is bounded.
is bounded.
- e)
-
![$l\colon[0,1]\to\mbox{{\bf R}}$](img969.gif) ,
, 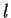 is continuous,
is continuous, 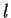 is not bounded.
is not bounded.




Next: 9.2 Intermediate Value Theorem
Up: 9. Properties of Continuous
Previous: 9. Properties of Continuous
Index
![]() is a maximizing set for
is a maximizing set for ![]() on
on ![]() , and
, and
![]() , then
, then ![]() is
also a maximizing set for
is
also a maximizing set for ![]() on
on ![]() .
.
![]() is any function (with
is any function (with
![]() ), then
), then ![]() is a
maximizing set for
is a
maximizing set for ![]() on
on ![]() , so every function with non-empty domain has a
maximizing set.
, so every function with non-empty domain has a
maximizing set.
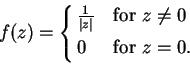
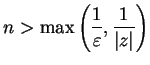 ; then
; then
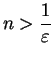 , so
, so
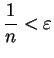 , so
, so
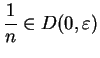 and
and
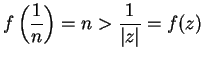 . This argument shows that
. This argument shows that
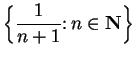 is also a maximizing set for
is also a maximizing set for ![]() is a maximizing set for
is a maximizing set for ![]() on
on ![]() , but
, but ![]() is not a
maximizing set for
is not a
maximizing set for ![]() on
on ![]() . Then there is some
. Then there is some ![]() such that for all
such that for all ![]() ,
, ![]() . Since
. Since ![]() is a maximizing set for
is a maximizing set for ![]() on
on ![]() ,
there is an element
,
there is an element ![]() in
in ![]() such that
such that ![]() , so
, so ![]() for all
for all ![]() , so
, so ![]() , so
, so ![]() . Now, for every
. Now, for every ![]() there is an element
there is an element ![]() in
in ![]() with
with
![]() . If
. If ![]() , then the element
, then the element ![]() satisfies
satisfies
![]() so
there is some element
so
there is some element ![]() with
with ![]() (if
(if ![]() , take
, take ![]() ;
if
;
if ![]() , take
, take ![]() .) Hence
.) Hence ![]() is a
maximizing set for
is a
maximizing set for ![]() on
on ![]() .
.
![]()
![]() with
with
![]() such that each interval
such that each interval ![]() is a maximizing set for
is a maximizing set for ![]() on
on
![]() . We put
. We put
![\begin{eqnarray*}[a_0,b_0]&=& [a,b] \cr
[a_{n+1},b_{n+1}] &=& \cases{
\left[ a_...
...r } f$\ \cr
\left[{{a_n+b_n}\over 2},b_n\right] &otherwise.\cr}
\end{eqnarray*}](img938.gif)
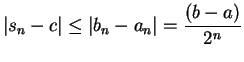 , so
, so ![]() such that
such that