Index A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | W | Z

A

absolute convergence

11.4

absolute summability

11.4

absolute value, of complex number

6.1

absolute value, product formula

2.7

absolute value, quotient formula for

2.7

absolute value

2.7

addition (field operation)

2.3

addition in $\mbox{{\bf Z}}_n$

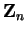
2.2

addition laws for sine and cosine

12.6

addition of inequalities

2.6

Alembert, Jean (1717-1783)

11.4

alternating series

11.3

alternating series test

11.3

ambiguous, $a^{b^c}$

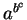
12.1

ambiguous, sequence notation

5.1

and, logical connective

1.2

Archimedean property

5.2 | 5.2 | 5.2 | 5.3

Archimedes

5.3

argument(of a complex number

12.6

Aristotle (384-322 B.C.)

2.3 | 3.2

Arnold cats

6.5

Arnold, Vladimir (1937-??)

6.5

Ars Magna

4.2

Artin, Emil (1898-1962)

2.7

associative operation

2.1

associative

2.2

associativity of $\oplus$

B.

associativity of $\odot$

4.1 | B.

axiom, completeness

5.2

axioms for a field

2.3

axioms, for ordered field

2.6

axioms

intro

axis, imaginary

6.2

axis, real

6.2

B

Bernoulli, Jacob (1654-1705)

2.3 | 11.4 | 11.4 | 12.9

between

9.2

Bhaskara (born 1114-1185)

3.1

binary operation

2.1

binary search sequence

5.1

Bolzano, Bernhard, (1781-1848)

9.2

Boole, George (1815-1864)

2.2

bound for a function

8.3

bound for a set

8.3

bound for sequence

7.5

bound, lower

7.8

bound, upper

7.8

bounded function

8.3

bounded sequence

7.5 | 7.5

bounded set

8.3

boundedness theorem

9.1

bug

2.2

Buhler, Joe (1950-??)

intro

C

calculator operations

2.2

cancellation law

2.1 | 2.4

Cardano, Girolamo (1501-1576)

2.7 | 4.2

Cartesian product

1.4

cat, Arnold

6.5

cat, discontinuous image of

8.3

cat, exponential of

12.6

cat, inverse of

6.5

cat, square of

6.5

Cauchy, Augustin(1789-1857)

3.5 | 4.2 | 9.2

chain rule

10.1

circle of convergence

12.2

circle,unit

6.2

circle

6.2

Clenias

3.2

closed interval

5.1

codomain of function

1.5

commensurable

3.2

commutative operation

2.1

commutative

2.2

commutativity of addition in field

2.4

comparison test (limit)

11.2

comparison test for series

11.2

comparison theorem for null sequences

7.3

complete

5.2

completeness axiom

5.2

completeness

5.3

complex conjugate

4.2

complex function

8.1

complex numbers

6.1

complexification

4.1

composition of continuous functions

8.2

composition of functions

8.2

composition

8.1

conjugate, complex

4.2

conjugate

4.2

constant sequence

7.1 | 7.2

continuity of 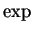$\exp$, (in theorem 12.27)

12.4

continuity of roots

8.2

continuity, of $\ln$

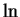
12.5

continuity

5.3

continuous at a point

8.2

continuous on a set

8.2

continuous

8.2

convergence of geometric sequence

7.6

convergence of geometric series

7.6

convergence of search sequence

5.1

convergence, absolute

11.4

convergence, circle of

12.2

convergence, disc of

12.2

convergence, radius of

12.2

convergence

7.2

convergent sequence, limit of

7.5

convergent sequence, product theorem

7.5

convergent sequence, reciprocal theorem

7.5

convergent sequence, sum theorem

7.5

convergent sequence, uniqueness theorem

7.5

convergent sequence

7.2

convergent sequences, quotient theorem

7.5

convergent sequences

7.5

copy (of 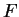in )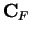

4.1

cosine, complex

11.4

cosine

12.3 | 12.7

critical point theorem

10.2

critical point

10.2

D

D'Alembert, Jean (1717-1783)

11.4

De Moivre's formula

6.2

De Moivre, Abraham (1667-1754)

6.5

decimal notation

7.6

decimals

intro

decomposition theorem

7.5

decreasing function

5.3

decreasing sequence

7.8

definition by recursion

3.3

derivative

10.1

Descartes, Rene, 1596-1650

3.5

Dickson, Leonard Eugene, (1874-1954

2.3

difference of sets

1.4

difference, symmetric

2.1

differential equation

12.4

differentiation of power series

12.3 | 12.8

digits

2.4

direction in $\mbox{{\bf C}}$

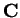
6.3

direction of complex number

6.3

disc of convergence

12.2

disc open

6.2

disc, closed

6.2

disc, unit

6.2

distance (in ordered field)

2.7

distributive law in $\mbox{{\bf Z}}_n$

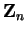
B.

distributive law in a field

2.5

distributive law

2.3

distributive

2.2

divergence of search sequence

5.1

divergence test

7.7

divergent sequence

7.2

division in a field

2.5

domain of function

1.5

double inverse theorem

2.1 | 2.4

draughts

3.2

dull sequence

7.3

E

$e$

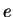
12.4 | 12.9

empty set

1.1

endpoints of an interval

2.7

entertainments

intro

Epicureans

6.2

equality of functions

1.5

equality of objects

1.3

equality of ordered pairs

1.4

equality of rules

1.5

equality of sets

1.1

equality, reflexive property

1.3

equality, substition property

1.3

equality, symmetric property

1.3

equality, transitive property

1.3

equivalence for sets of propositions

2.5

equivalence of propositions

1.2

Euclid (365-300BC??)

3.1 | 3.2 | 3.2 | 5.3 | 6.2

Euler, Leonard (1707-1783)

4.2 | 6.5 | 11.2 | 12.9

Euler, summation notation

3.5

even integer

3.2

even number

3.1

exercises

intro

exponential function

12.4

exponents, laws for fractional

5.3

exponents, rational

5.3

extreme value theorem

9.1

F

factorial function

3.3

factorial

3.5

factorization of $a^p-r^p$

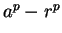
3.4

factorization (depends on field)

3.4

feature

2.2

field, axioms for

2.3

field, orderable

2.6

field, real

5.2

function, complex

8.1

function, increasing and decreasing

5.3

function, recursive

3.3

function

1.5

functions, addition and multiplication of

5.3

G

Göttingen

11.4

Gauss, Carl (1777-1855)

12.7

geometric sequence, convergence of

7.6

geometric sequence

7.1 | 11.1

geometric series, convergence of

7.6

geometric series

3.4

geometric series

7.1 | 11.1

graph

5.3

Gregory, John (1638-1675)

11.4 | 12.9

H

Hamilton, William R. (1805-1865)

2.2 | 4.2

harmonic series

11.1 | 11.4

Huntington, Edward (1874-1952)

2.5 | 2.7

hyperbolic functions

12.6

I

identity element for binary operation

2.1

image of a function

6.5

imaginary axis

6.2

imaginary part of complex number

6.1

implication

1.2

incommensurables

3.2 | 3.2

increasing function

5.3

increasing sequence

7.8

induction theorem (generalized)

3.1

induction theorem

3.1

inductive

3.1

inequalities, addition of

2.6

inequalities, multiplication of

2.6

inequality theorem

7.7

inequality, triangle

2.7

infinite series

11.1

integer, even

3.2

integer, odd

3.2

integers in a field

3.2

integers, informal definition

1.1

integers

3.2

interior point

10.2

interior

10.2

intermediate value theorem

9.2 | 9.2 | 9.2

intersection

1.4

interval, closed or open

5.1

interval

2.7

inverse for binary operation

2.1

inverse of cat

6.5

invertible element for binary operation

2.1

J

Jones, William, (1675-1749)

12.9

K

Koch, Helge von (1870-1924)

7.8

Kramp, Christian, 1760-1826

3.5

L

Lagrange, Joseph, (1736-1813)

11.4

Landau, Edmund (1877-1938)

11.4

The Laws

3.2

laws of exponents (fractional)

5.3

laws of signs

2.6

Laws of Thought

2.2

least element principle

3.1

Leibniz, Gottfried (1646-1716)

11.4 | 11.4 | 12.9

length of complex number

6.3

limit comparison test

11.2

limit of a function

8.3

limit of sequence

7.5

limit point

8.3

limit, uniqueness of

8.3

line segment

10.2

logarithm

12.5

lower bound for a set

9.1

lower bound for sequence

7.8

M

Madhava of Sangamagramma (c. 1340-1425)

10.3 | 11.4 | 12.9

Mahavira (ninth century)

3.1

Maple

2.2 | 3.5 | 3.5 | 4.2 | 12.6 | 12.9 | 12.9

maps to

7.1

Mathematica

3.5 | 3.5 | 4.2 | 12.6 | 12.9 | 12.9

maximizing set

9.1

maximum function

3.5 | 3.5

maximum, critical point theorem

10.2

maximum

9.1

mean value theorem

10.2

Mercator, Nicolaus(1620-1687)

11.4

midpoint

5.1

minimum

9.1

monotonic sequence

7.8

multiplication (field operation)

2.3

multiplication in $\mbox{{\bf Z}}_n$

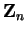
2.2

multiplication of inequalities

2.6

multiplication table

2.2

Mycielski, Jan

7.8

N

natural numbers, informal definition

1.1

natural numbers

3.1 | 3.2

negative elements in ordered field

2.6

Newton, Isaac (1643-1727)

5.3 | 10.3 | 11.4

not, negation

1.2

null sequence, comparision theorem

7.3

null sequence, root theorem

7.3

null sequence, sum theorem

7.4

null sequence

7.3

null sequences, product theorem

7.4

null-times-bounded theorem

7.5

number, odd

3.1

number, even

3.1

numbers natural

3.2

numbers, complex

6.1

numbers, natural

3.1

numbers, rational

3.2

numbers, real

5.2

O

odd integer

3.2

odd number

3.1

open interval

5.1

opposite sign

2.6

or, logical connective

1.2

orderable field

2.6

ordered field, axioms for

2.6

ordered field, completemess of

5.2

ordered pair

1.4

ordered triple

1.4

Oresme, Nicole (1323-1382)

11.4

P

pair, ordered

1.4

paradox

1.6

parentheses

2.3

Pascal, Blaise (1623-1662)

3.1

path

10.2

Peano,Giuseppe (1858-1932)

3.1

periodicity of $\exp$

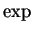
12.6

periodicity of 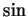$\sin$ and $\cos$,

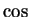12.59A h) and i) | 12.6

Philitas of Cos

1.6

pi

12.6 | 12.9

Plato (427?-347B.C.), The Laws

3.2

polar decomposition

6.3

polygon representation for a complex sequence

7.1

polygon, snowflake

7.6

positive elements in ordered field

2.6

power function

3.3 | 3.5

power rule for differentiation

10.1

power series

12.1

power, integer

3.3

precedence

2.3

precision function

7.3 | 7.8

Priora Analytica

3.2

Proclus

6.2

product formula for absolute value

2.7

product of functions

5.3

product rule for differentiation

10.1

product theorem for null sequences

7.4

product theorem for continuous functions

8.2

product theorem for convergent sequences

7.5

product theorem for limits of functions

8.3

proposition form

1.4

proposition

1.2

propositions, equivalence of

1.2

Pythagorean theorem

6.2

Q

quadratic formula

2.5

quotient formula for absolute value

2.7

quotient rule for differentiation

10.1

quotient theorem for continuous functions

8.2

quotient theorem for convergent sequences

7.5

quotient, of functions

5.3

R

radius of convergence

12.2

ratio for a geometric sequence

7.1

ratio for geometric series

7.1

ratio test

11.2 | 11.4

rational exponents

5.3

rational numbers in a field

3.2

rational numbers, informally defined

1.1

rational numbers

3.2

rational, (in sense of Euclid)

3.2

real axis

6.2

real field

5.2

real part of comlex number

6.1

reciprocal rule for differentiation

10.1

reciprocal theorem for convergent sequences

7.5

recursion

3.3

Reed College

intro

restriction theorem

10.2

reverse triangle inequality

7.5

Rolle's theorem

10.2

Rolle, Michel (1672-1719)

10.3

root of complex number

6.3

root of real number (theorem 5.49)

5.3

root theorem for null sequences

7.3

roots of complex numbers

12.6

roots, continuity of

8.2

rule, recursive

3.3

Russell's paradox

1.6

Russell, Bertrand 1872-1970

1.6

S

Sangamagramma, Madhava (c. 1340-1425)

10.3

Schreier, Otto (1901-1929)

2.7

search sequence, convergence of

5.1

search sequence

5.1

segment

10.2

sequence, bounded

7.5 | 7.5

sequence, constant

7.1 | 7.2

sequence, convergent

7.2 | 7.2 | 7.5

sequence, decreasing

7.8

sequence, divergent

7.2

sequence, dull

7.3

sequence, increasing

7.8

sequence, lower bound

7.8

sequence, null

7.3

sequence, search

5.1

sequence, summable

11.1

sequence, upper bound

7.8

sequence

5.1 | 7.1

series alternating

11.3

series operator

11.1

series, power series

12.1

series, sum of

11.1

series

11.1

Servois, Francois-Joseph (1767-1847)

2.2

set

1.1

set difference

1.4

set empty

1.1

sine, complex

11.4

sine

12.3 | 12.7

Skolem functions

7.8

snowflake

7.6 | 7.8

square $(x\cdot x)$

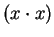
2.5

square root of complex number

6.4

square root

2.6

subset

1.1 | 1.1

substition property of equality

1.3

subtraction in a field

2.5

sum of a series

11.1

sum of functions

5.3

sum theorem for continuous functions

8.2

sum theorem for convergent sequences

7.5

sum theorem for differentiable functions

10.1

sum theorem for limits of fumctions

8.3

sum theorem for null sequences

7.4

sum theorem for series

11.1

summable sequence

11.1

summable, absolutely

11.4

summation function

3.5

summation

3.4

symmetric difference

2.1

T

transitivity of $<$

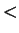
2.6

transitivity of equality

1.3

transitivity of implication

1.2

translate of a sequence

7.7

translation theorem

7.7

triangle inequality , in $\mbox{{\bf C}}$

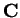
6.1

triangle inequality, reverse

7.5

triangle inequality

2.7 | 6.2

trichotomy

2.6

trigonometric functions

11.4 | 12.3 | 12.6 | 12.7

triple, ordered

1.4

U

union

1.4

uniqueness of $\mbox{{\bf R}}$

5.2

uniqueness of identities

2.1

uniqueness of inverses

2.1

uniqueness of limits

8.3

uniqueness theorem for convergent sequences

7.5

unit circle

6.2

unit disc

6.2

upper bound for a set

9.1

upper bound for sequence

7.8

W

Waring, Edward, (1734-1798)

11.4

Weber, Heinrich Martin (1842-1913)

2.5

Weierstrass, Karl (1815-1897)

2.7 | 9.2

Z

zero-one law

2.3