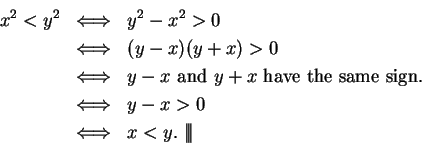Next: 2.7 Absolute Value
Up: 2. Fields
Previous: 2.5 Subtraction and Division
Index
2.101
Example.
The rational numbers
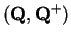
form an ordered field, where
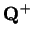
denotes
the familiar set of positive rationals.
2.102
Notation ( .)
.)
Let
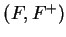
be an ordered field. We let
We call
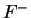
the set of
negative elements in
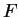
. Thus
and
We can restate the Trichotomy axiom as: For all
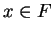
, exactly one of the
statements
is true.
2.103
Theorem.
Let 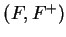 be an ordered field. Then for all
be an ordered field. Then for all
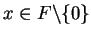 ,
, 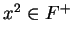 .
.
Proof: Since 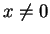 , we know
, we know 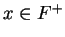 or
or 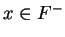 . Now
. Now
and
2.104
Corollary.
In any ordered field, 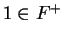 .
.
2.106
Remark.
The method used in the second proof above shows that none of the fields
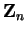
are orderable.
2.107
Definition (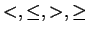 )
)
Let
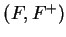
be an ordered field, and let
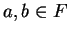
. We define
2.108
Remark.
In any ordered field
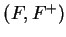
:
2.109
Exercise.
Let
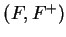
be an ordered field, and let
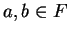
. Show that exactly one of
the statements
is true.
2.110
Theorem (Transitivity of 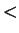 .)
Let
.)
Let 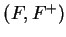 be an ordered field. Then for all
be an ordered field. Then for all 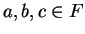 ,
,
Proof: For all 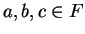 we have
we have
2.111
Exercise (Addition of inequalities.)
Let
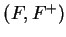
be an ordered field, and let
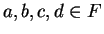
. Show that
and
2.112
Exercise.
Let
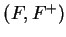
be an ordered field, and let
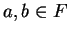
. Show that
2.113
Notation.
Let
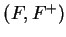
be an ordered field, and let
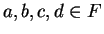
. We use notation like
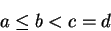 |
(2.114) |
to mean
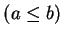
and
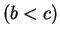
and
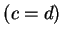
, and similarly we write
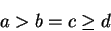 |
(2.115) |
to mean
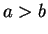
and
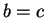
and
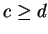
. By transitivity of
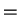
and of
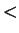
, you can
conclude
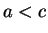
from (
2.114), and you can conclude
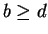
and
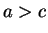
from
(
2.115). A chain of inequalities involving both
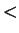
and
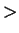
shows bad
style, so you should not write
2.116
Exercise (Laws of signs.)
Let
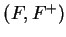
be an ordered field, and let
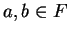
. Show that
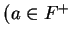 and
and
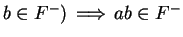
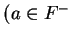 and
and
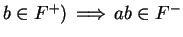
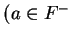 and
and
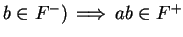
These laws together with the axiom
are called the
laws of signs.
2.117
Notation.
Let
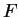
be an ordered field, and let
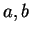
be non-zero elements of
. We say
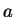
and
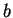 have the same sign
have the same sign if either (
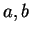
are both in
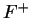
) or (
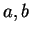
are both in
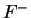
). Otherwise we say
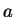 and
and 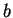 have opposite signs
have opposite signs.
2.118
Corollary (of the law of signs.)Let 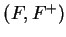 be an ordered field and let
be an ordered field and let
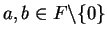 . Then
. Then
2.119
Notation.
I will now start to use the convention that `` let
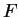
be an ordered field" means ``let
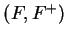
be an ordered field''; i.e.,
the set of positive elements of
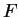
is assumed to be called
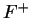
.
2.120
Exercise.
Let
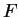
be an ordered field and let
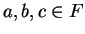
. Prove that
2.121
Theorem (Multiplication of inequalities.)Let 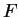 be an ordered field and let
be an ordered field and let 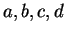 be elements of
be elements of 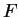 . Then
. Then
Proof: By the previous exercise we have
Hence, by transitivity of 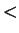 ,
,
2.122
Exercise.
Let
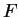
be an ordered field, and let
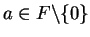
. Show that
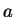
and
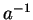
have the same sign.
2.123
Exercise.
A
Let
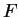
be an ordered field, and let
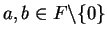
.
Under what conditions (if any) can you say that
Under what conditions (if any) can you say that
2.124
Definition (Square root.)
Let
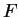
be a field, and let
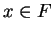
. A square root for
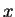
is any element
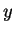
of
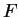
such that
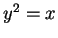
.
2.125
Examples.
In
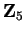
, the square roots of
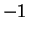
are
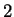
and
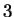
.
In an ordered field 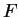 , no element in
, no element in 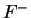 has a square root.
has a square root.
In
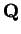 , there is no square root of
, there is no square root of 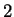 . (See theorem 3.45
for a proof.)
. (See theorem 3.45
for a proof.)
2.126
Theorem.
Let 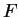 be an ordered field and let
be an ordered field and let 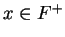 . If
. If 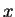 has a square root, then it
has exactly two square roots, one in
has a square root, then it
has exactly two square roots, one in 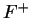 and one in
and one in 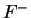 , so if
, so if 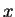 has a square
root, it has a unique positive square root.
has a square
root, it has a unique positive square root.
Proof: Suppose 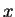 has a square root
has a square root 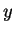 . Then
. Then 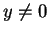 , since
, since 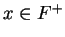 . If
. If 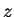 is any square root of
is any square root of 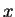 , then
, then 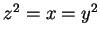 , so, as we saw in theorem 2.95,
, so, as we saw in theorem 2.95,
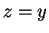 or
or 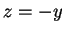 . By trichotomy, one of
. By trichotomy, one of 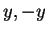 is in
is in 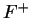 , and the other is in
, and the other is in
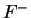 .
.
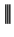
Proof: Let 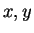 be elements of
be elements of 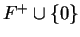 . Then
. Then 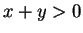 , unless
, unless 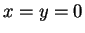 ,
so
,
so
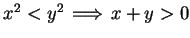 . Hence
. Hence
2.129
Remark.
The implication (
2.128) is also true when
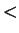
is replaced by
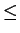
in both
positions. I'll leave this to you to check.




Next: 2.7 Absolute Value
Up: 2. Fields
Previous: 2.5 Subtraction and Division
Index
![]() , we know
, we know ![]() or
or ![]() . Now
. Now
![]() of
of
![]() such that
such that
![]() were an ordered field, we would have
were an ordered field, we would have
![]() . But in
. But in
![]() ,
, ![]() so
so
![]() and
and
![]() , which contradicts trichotomy.
, which contradicts trichotomy.
![]()
![]() were an ordered field, we would
have
were an ordered field, we would
have
![]() , so
, so
![]() , so
, so
![]() , so
, so
![]() so
so
![]() . This contradicts trichotomy.
. This contradicts trichotomy.
![]()
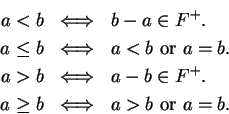
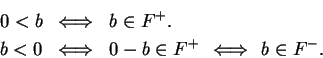
![]() we have
we have
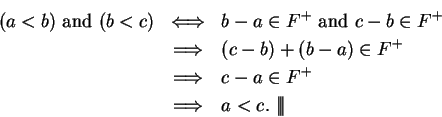
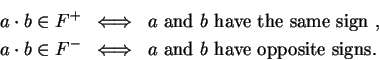
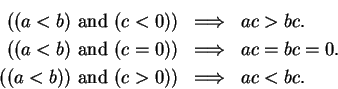
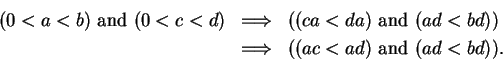
![]() , no element in
, no element in ![]() has a square root.
has a square root.
![]() , there is no square root of
, there is no square root of ![]() . (See theorem 3.45
for a proof.)
. (See theorem 3.45
for a proof.)
![]() has a square root
has a square root ![]() . Then
. Then ![]() , since
, since ![]() . If
. If ![]() is any square root of
is any square root of ![]() , then
, then ![]() , so, as we saw in theorem 2.95,
, so, as we saw in theorem 2.95,
![]() or
or ![]() . By trichotomy, one of
. By trichotomy, one of ![]() is in
is in ![]() , and the other is in
, and the other is in
![]() .
.
![]()
![]() be elements of
be elements of ![]() . Then
. Then ![]() , unless
, unless ![]() ,
so
,
so
![]() . Hence
. Hence