



Next: 8. Continuity
Up: 7. Complex Sequences
Previous: 7.7 The Translation Theorem
Index
7.87
Theorem.
Let ![$\{[a_n,b_n]\}$](img492.gif) be a binary search sequence in
be a binary search sequence in
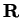 .
Suppose
.
Suppose
![$\{[a_n,b_n]\} \to c$](img493.gif) where
where
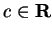 .Then
.Then 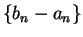 is a null sequence. Also
is a null sequence. Also 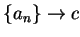 and
and 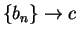 .
.
Proof: We know that
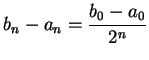 , and that
, and that
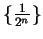 is a null sequence, so
is a null sequence, so
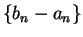 is
a null sequence. Since
is
a null sequence. Since
![$\{[a_n,b_n]\} \to c$](img493.gif) we know that
we know that
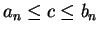 for all
for all
 , and hence
, and hence
for all
 . By the comparison theorem for null sequences
it follows that
. By the comparison theorem for null sequences
it follows that 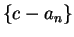 and
and 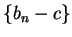 are null sequences, and hence
are null sequences, and hence
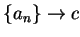 and
and
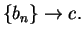

7.88
Definition (Increasing, decreasing, monotonic)
Let

be a real sequence. We say

is
increasing if
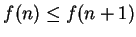
for all

, and we say

is
decreasing if
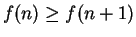
for
all

.
We say that

is
monotonic if either

is increasing
or

is decreasing.
7.89
Theorem.
Let  be an increasing real sequence. Then
for all
be an increasing real sequence. Then
for all
Proof: Define a proposition form 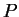 on
on
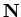 by
by
Then 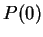 says ``for all
says ``for all
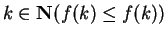 '', so
'', so 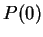 is true.
Since
is true.
Since  is increasing, we have for all
is increasing, we have for all
 ,
,
By induction, we conclude that 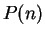 is true for all
is true for all
 , i.e.
, i.e.
Proof: For all
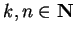
7.92
Definition (Upper bound, lower bound.)
Let

be a real sequence. We say that

has an
upper bound
if there is a number
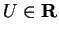
such that
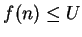
for all

. Any such number
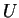
is called an
upper bound
for 
.
We say that

has a
lower bound
if there is a number
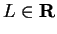
such that
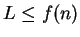
for all

.
Any such number
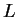
is called a
lower bound for 
.
7.93
Examples.
If
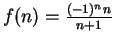
for all

then
(or any number greater than
) is an upper
bound for

, and
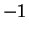
(or any number less than
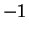
)
is a lower bound for

. The sequence
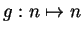
has no upper bound, but
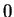
is a lower bound for
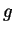
.
7.94
Exercise.
A
In definition
7.41,
we defined a complex
sequence

to bounded if there is a number
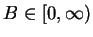
such that
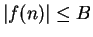
for all

. Show that a real sequence is bounded if and
only if it has both an upper bound and a lower bound.
7.95
Theorem (Bounded monotonic sequences converge.)Let  be
be
an increasing sequence in
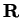 , and suppose
, and suppose  has an upper bound. Then
has an upper bound. Then
 converges. (Similarly, decreasing sequences that have lower bounds converge.)
converges. (Similarly, decreasing sequences that have lower bounds converge.)
Proof: Let 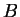 be an upper bound for
be an upper bound for  . We will construct a binary search
sequence
. We will construct a binary search
sequence ![$\{[a_n,b_n]\}$](img492.gif) satisfying the following two conditions:
satisfying the following two conditions:
i. For every
 ,
, 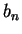 is an upper bound for
is an upper bound for  ,
,
ii. For every
 ,
, 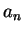 is not an upper bound for
is not an upper bound for  .
.
Let
A straightforward induction argument shows that ![$\{[a_n,b_n]\}$](img492.gif) satisfies conditions i) and ii).
satisfies conditions i) and ii).
Let 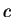 be the number such that
be the number such that
![$\{[a_n,b_n]\} \to c$](img493.gif) . I will show that
. I will show that 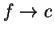 .
.
We know that
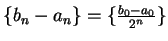 is a null sequence.
Let
is a null sequence.
Let  be a precision function for
be a precision function for 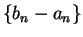 , so that for all
, so that for all
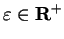 ,
,
I will use 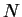 to construct a precision function
to construct a precision function 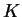 for
for 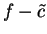 .
.
Let
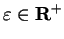 . Since
. Since
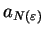 is not an upper bound for
is not an upper bound for  ,
there is a number
,
there is a number
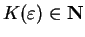 such that
such that
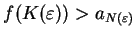 .
By condition i), I know that
.
By condition i), I know that
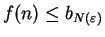 for all
for all
 .
Hence, since
.
Hence, since  is increasing, we have
for all
is increasing, we have
for all
 :
:
Since
![$\{[a_n,b_n]\} \to c$](img493.gif) we also have
we also have
Hence
This says that  is a precision function for
is a precision function for 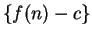 , and hence
, and hence
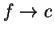

7.97
Example.
Let
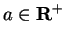
. Define a sequence
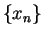
by
We have
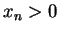
for all
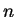
.
Suppose
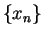
converges to a limit
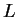
.
Since
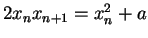
for all

, we can use
the translation theorem to show that
so
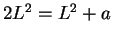
, and hence
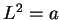
, so
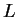
must be
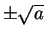
. Since
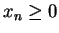
for all
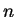
, it follows from the inequality theorem that
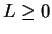
, and hence if
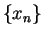
converges, it must converge to
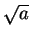
. In order to show that
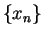
converges, it is sufficient to show that
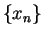
is decreasing. (We've already noted
that
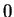
is a lower bound.)
Well,
so if I can show that
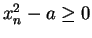
for all

, then I'll know that
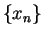
is decreasing. Now
I also note that
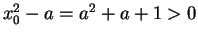
, so I finally conclude that
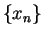
is
decreasing, and hence
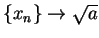
. In fact, this sequence converges very
fast, and is the basis for the square root algorithm used on most computers.
7.98
Example (
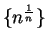 )
)
We will show that
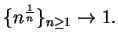
Claim:
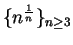 is a decreasing sequence.
is a decreasing sequence.
Proof: For all
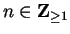 ,
,
We will show by induction that (
7.99) holds for all
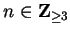
.
Let
Then
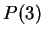
says
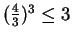
, which is true since
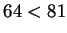
.
For all
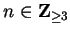
,
By induction,
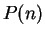
is true for all
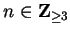
,
and the claim is proved.
Let
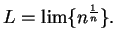 Then
Then
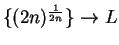 , since any precision function for
, since any precision function for
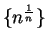 is also a precision function for
is also a precision function for
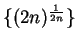 .
Hence
.
Hence
Thus
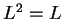
, and hence
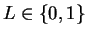
. Since
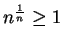
for all
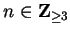
it follows from the inequality
theorem that
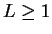
, and hence
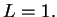

7.100
Exercise.
A
Show that
the sequence
is a null sequence.
7.101
Exercise.
Criticize the following argument.
We know that
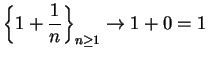 .
.
Hence
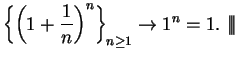
7.102
Note.I got the idea of using precision functions
from a letter by Jan Mycielski in the
Notices of the American Mathematical
Society[
34, p 569]. Mycielski calls precision functions
Skolem functions.
The snowflake was introduced by Helge von Koch(1870-1924)
who published his results
in 1906 [32]. Koch considered only the part of the boundary
corresponding to the bottom third of our polygon, which he introduced
as an example of a curve not having a tangent at any point.
The sequence  from Exercise 7.82 is taken from
[12, page 55, ex 20]
from Exercise 7.82 is taken from
[12, page 55, ex 20]




Next: 8. Continuity
Up: 7. Complex Sequences
Previous: 7.7 The Translation Theorem
Index
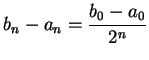 , and that
, and that
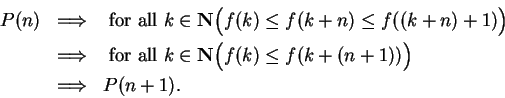
![]()
![]() be an upper bound for
be an upper bound for ![]() . We will construct a binary search
sequence
. We will construct a binary search
sequence ![]() satisfying the following two conditions:
satisfying the following two conditions:
![]() ,
, ![]() is an upper bound for
is an upper bound for ![]() ,
,
![]() ,
, ![]() is not an upper bound for
is not an upper bound for ![]() .
.
![\begin{eqnarray*}[a_0,b_0]&=&[f(0) - 1,B]\cr
[a_{n+1},b_{n+1}]&=&
\cases{ \left[...
...ght] & if ${{a_n+b_n}\over 2}$\ is
not an upper bound for $f$.}
\end{eqnarray*}](img527.gif)
![]() satisfies conditions i) and ii).
satisfies conditions i) and ii).
![]() be the number such that
be the number such that
![]() . I will show that
. I will show that ![]() .
.
![]() is a null sequence.
Let
is a null sequence.
Let ![]() be a precision function for
be a precision function for ![]() , so that for all
, so that for all
![]() ,
,
![]() . Since
. Since
![]() is not an upper bound for
is not an upper bound for ![]() ,
there is a number
,
there is a number
![]() such that
such that
![]() .
By condition i), I know that
.
By condition i), I know that
![]() for all
for all
![]() .
Hence, since
.
Hence, since ![]() is increasing, we have
for all
is increasing, we have
for all
![]() :
:
![\begin{eqnarray*}
n \geq K(\varepsilon) & \mbox{$\Longrightarrow$}& a_{N(\vareps...
...rightarrow$}& f(n) \in [a_{N(\varepsilon)}, b_{N(\varepsilon)}].
\end{eqnarray*}](img538.gif)
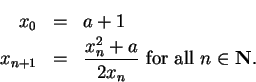
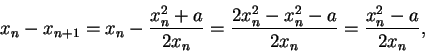
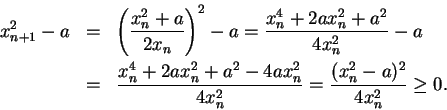
![]() is a decreasing sequence.
is a decreasing sequence.
![]() ,
,
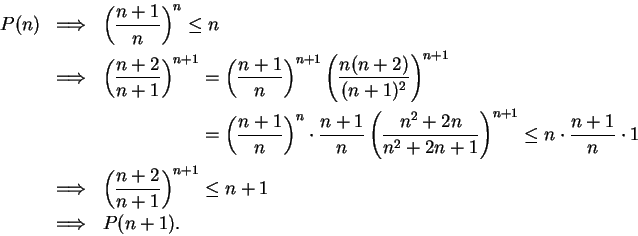
![]() Then
Then
![]() , since any precision function for
, since any precision function for
![]() is also a precision function for
is also a precision function for
![]() .
Hence
.
Hence
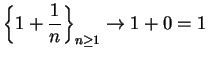 .
.
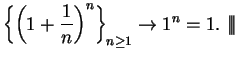
![]() from Exercise 7.82 is taken from
[12, page 55, ex 20]
from Exercise 7.82 is taken from
[12, page 55, ex 20]