We say
It appears from figure a 7.1 that for every disc ![]() centered at
centered at ![]() the
terms of the sequence
the
terms of the sequence
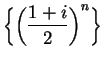 eventually get into
eventually get into ![]() ; i.e., it appears that
; i.e., it appears that
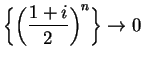 . Similarly, it
appears that
. Similarly, it
appears that
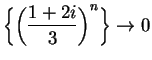 .
.
From figure b, it appears that there are numbers ![]() such that
such that
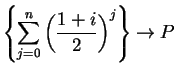 , and
, and
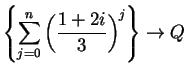 . You should
be able to put your finger on
. You should
be able to put your finger on ![]() and
and ![]() , and maybe to guess what their exact values
are. We will return to these examples later.
, and maybe to guess what their exact values
are. We will return to these examples later.
Let
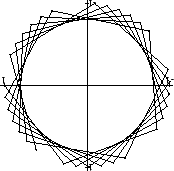
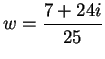 . The figure below represents the sequence
. The figure below represents the sequence
![]() . It appears from the figure that there is no number
. It appears from the figure that there is no number ![]() such that
such that
![]() . The following theorem shows that this is the case.
(Note that
. The following theorem shows that this is the case.
(Note that
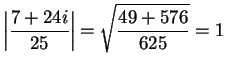 .)
.)
Proof: Suppose that ![]() and
and ![]() . Then for all
. Then for all
![]() ,
,
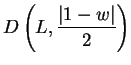 , there is a number
, there is a number
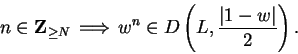
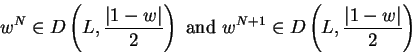
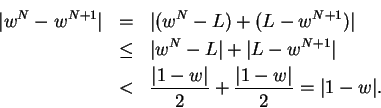
We can also show that constant sequences converge.
Proof: Let
![]() . Let
. Let ![]() be a disc centered at
be a disc centered at ![]() .
Then
.
Then
For purposes of calculation it is sometimes useful to rephrase the definition of
convergence. Since the disc ![]() is determined by its radius
is determined by its radius ![]() , and for
all
, and for
all
![]() ,
,
![]() , we can reformulate definition
7.6 as
, we can reformulate definition
7.6 as