By comparing this definition with definition 7.10, you see that
The definitions of null sequence and dull sequence use the same words, but they are not in the same order, and the definitions are not equivalent.
If ![]() satisfies condition (7.12), then whenever
satisfies condition (7.12), then whenever ![]() ,
,
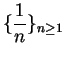 is
a null sequence, so null sequences are not necessarily dull.
is
a null sequence, so null sequences are not necessarily dull.
Proof:
Let
![]() . By the Archimedean property for
. By the Archimedean property for
![]() , there is an
, there is an
![]() such that
such that
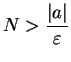 .
Then for all
.
Then for all
![]() ,
,
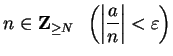 .
.
The difference between a null sequence and a dull sequence is that the `` ![]() " in
the definition of null sequence can (and usually does) depend on
" in
the definition of null sequence can (and usually does) depend on ![]() , while
the ``
, while
the ``![]() " in the definition of dull sequence depends only on
" in the definition of dull sequence depends only on ![]() . To emphasize
that
. To emphasize
that ![]() depends on
depends on ![]() (and also on
(and also on ![]() ), I will often write
), I will often write
![]() or
or
![]() instead of
instead of ![]() .
.
Here is another reformulation of the definition of null sequence.
This formulation shows that in order to show that a sequence ![]() is a null sequence, you need to find a function
is a null sequence, you need to find a function
![]() such that
such that
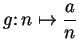 we had
we had

Proof: If ![]() , then
, then
![]() . Suppose, to get a
contradiction, that
. Suppose, to get a
contradiction, that ![]() is a null sequence. Then there is a number
is a null sequence. Then there is a number
![]() such that for all
such that for all
![]() . Then for all
. Then for all
![]() ,
,
If ![]() then (7.16) is false and this shows that
then (7.16) is false and this shows that ![]() is not a null
sequence.
is not a null
sequence.
![]()
Proof: Since ![]() is a null sequence, there is a function
is a null sequence, there is a function
![]() such
that for all
such
that for all
![]() ,
,
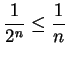 for all
for all
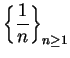 is a null sequence, it follows from the comparison theorem that
is a null sequence, it follows from the comparison theorem that
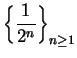 is a null sequence. Also, since
is a null sequence. Also, since
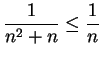 for all
for all
 is a null sequence.
is a null sequence.
Scratchwork: Let
![]() . I want to find
. I want to find ![]() so that for all
so that for all
![]() and all
and all
![]() ,
,
Proof: Let ![]() be a null sequence in
be a null sequence in ![]() and let
and let ![]() be a precision
function for
be a precision
function for ![]() . Define
. Define
![]() by
by
![]() for all
for all
![]() . Then for all
. Then for all
![]() ,
,
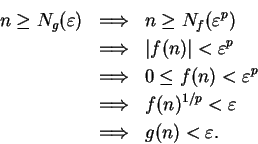
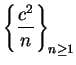 is a null
sequence in
is a null
sequence in  is a
null sequence.
is a
null sequence.
Consider the sequence
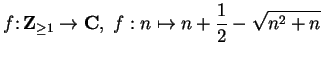 . For all
. For all
![]() ,
,
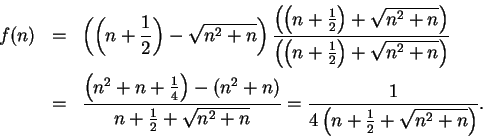
 , so it follows from the
comparison theorem that
, so it follows from the
comparison theorem that
Since
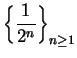 is a null sequence, it follows
from the root theorem that
is a null sequence, it follows
from the root theorem that
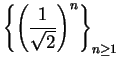 is a null sequence. Now
is a null sequence. Now
 ,
so
,
so
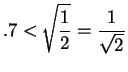 so
so
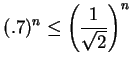 for all
for all
![]() , and by another comparison test,
, and by another comparison test,
![]() is a null sequence. Since
is a null sequence. Since
![]() ,
it follows that
,
it follows that
![]() is a null sequence for all
is a null sequence for all
![]() with
with
![]() .
.
You probably suspect that ![]() is a null sequence for all
is a null sequence for all
![]() with
with ![]() . This is correct, but we will not prove it yet.
. This is correct, but we will not prove it yet.
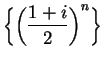 and
and
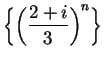 that are sketched above 7.1 are in fact
null sequences.
that are sketched above 7.1 are in fact
null sequences.
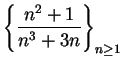
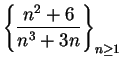
It follows from remark 5.38 that we can add, subtract and multiply complex
sequences, and that the usual associative, commutative, and distributive laws hold.
If ![]() and
and ![]() then
then
![]() and
and
![]() . If
. If
![]() then the constant sequences
then the constant sequences
![]() satisfy
satisfy
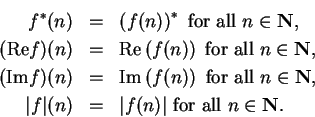
Proof: All four results follow by the comparison theorem. We have, for all
![]() :
:
