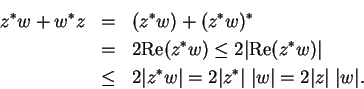6.2
Definition (Absolute value.)
In exercise
4.23A we showed that (for any field
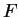
in which
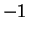
is not a
square), if
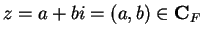
, then
If we are working in

, then
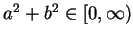
and hence
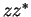
has a unique
square root in
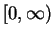
, which we denote by
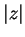
and call the
absolute
value of
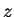
.
We note that
Also note that for
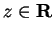
, this definition agrees with our old definition of
absolute value in
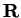
.
6.5
Exercise.
Prove parts b), c), d), e), f), g), h) and i) of Theorem
6.4.
A
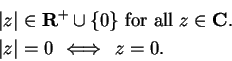
![]() ,
,